题目内容
已知A，B是两个锐角，且满足sin2A+cos2B=
t，cos2A+sin2B=
t，则实数t所有可能值的和为 ．
| 5 |
| 4 |
| 3 |
| 4 |
考点：同角三角函数的关系
专题：
分析：根据同角的正弦的平方加它的余弦的平方等于1，等式的性质，可得关于t的方程，根据解方程，可得答案．
解答：解：由A，B是两个锐角，且满足sin2A+cos2B=
t，cos2A+sin2B=
t，得
sin2A+cos2B+cos2A+sin2B=
t+
t．
化简，得（sin2A+cos2A）+（sin2B+cos2B）=
t+
t．
由同角的正弦的平方加它的余弦的平方等于1，得
t+
t=2．
2t=2．解得t=1，
故答案为：1．
| 5 |
| 4 |
| 3 |
| 4 |
sin2A+cos2B+cos2A+sin2B=
| 3 |
| 4 |
| 5 |
| 4 |
化简，得（sin2A+cos2A）+（sin2B+cos2B）=
| 3 |
| 4 |
| 5 |
| 4 |
由同角的正弦的平方加它的余弦的平方等于1，得
| 3 |
| 4 |
| 5 |
| 4 |
2t=2．解得t=1，
故答案为：1．
点评：本题考查了同角三角函数的关系，利用了同角的正弦的平方加它的余弦的平方等于1．
练习册系列答案
相关题目
如图．在△ABC中，∠C=90°，AC=8，AB=10，点P在线段AC上运动，若圆O的半径是y，AP=x，且⊙0的圆心在线段BP上，圆O与AB，AC都相切．请求出y与x的函数关系式．
（黑线表示被弟弟涂掉的部分），请你将这道作业题补充完整，并列方程解答．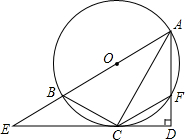
如图，Rt△ADE中，∠D=90°，点O为斜边上一点，以AB为直径的⊙O交ED于点C，连接CA、CB、CF，
如图所示，从∠1，∠2，∠3，∠4，∠A，∠C，∠ABC，∠ADC中，找出所有的内错角和同旁内角．
如图所示，AB，AC为⊙O的两弦，D为