Question

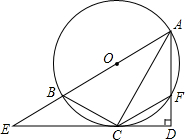如图，Rt△ADE中，∠D=90°，点O为斜边上一点，以AB为直径的⊙O交ED于点C，连接CA、CB、CF，

BC

=

CF

，
（1）求证：DE为⊙O的切线；
（2）求证：AF+2DF=AB．

Answer 1

考点：切线的判定

专题：

分析：（1）连接OC，根据条件可证明∠OCA=∠CAF，可证得OC∥AD，由条件可得出OC⊥DE，可得结论；
（2）过C作CM⊥AB于M，可证明△AMC≌△ADC，△BMC≌△FDC，可证得结论．

解答：证明：
（1）如图1，连接OC，

∵OA=OC，
∴∠OCA=∠OAC，
∵

BC

=

CF

，
∴∠OAC=∠CAD，
∴∠OCA=∠CAD，
∴OC∥AD，
∵∠D=90°，
∴∠OCE=90°，即OC⊥DE，
∴DE是⊙O的切线；
（2）如图2，过C作CM⊥AB于M，

∵

BC

=

CF

，
∴∠MAC=∠DAC，
在△MAC和△DAC中

∠MAC=∠DAC ∠CMA=∠D AC=AC

∴△MAC≌△DAC（AAS），
∴AM=AD，CM=CD，
∵

BC

=

CF

，
∴BC=CF，
在Rt△BCM和Rt△FCD中

BC=CF CM=CD

∴Rt△BCM≌Rt△FCD（HL），
∴BM=FD，
∴AB=AM+BM=AD+DF=AF+2DF，
即AF+2DF=AB．

点评：本题主要考查切线的性质和判定及全等三角形的判定和性质，掌握切线的两种证明方法，即①有切点时，连接圆心和切点证明垂直，②无切点时作垂直，证明距离等于半径是解题的关键．