题目内容
17.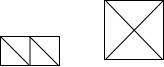 如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.
如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.
分析 由题意和图示可知,将两个边长为$\sqrt{3}$的正方形沿对角线剪开,将所得的四个三角形拼成一个大正方形,大正方形的边长恰好是小正方形的对角线的长,根据正方形的性质,利用勾股定理求出小正方形对角线的长即可.
解答 解:∵小正方形的边长为$\sqrt{3}$,
∴其对角线的长为$\sqrt{(\sqrt{3})^{2}+(\sqrt{3})^{2}}=\sqrt{6}$.
故答案为:$\sqrt{6}$
点评 此题主要考查算术平方根,关键是学生对正方形性质和勾股定理的理解和掌握.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
8.△DEF是由△ABC平移得到的,点A(-2,-1)的对应点为D(1,-3),则点C (2,3)的对应点F的坐标为( )
| A. | (-1,5) | B. | (1,5) | C. | (5,1) | D. | (5,-4) |
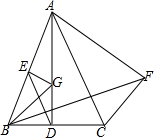 如图,△ABC中,AB=AC,D,E分别是BC,AB的中点,作BF⊥AC且使BF=AC,BG平分∠ABF.
如图,△ABC中,AB=AC,D,E分别是BC,AB的中点,作BF⊥AC且使BF=AC,BG平分∠ABF.
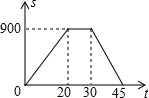 乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图.
乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图.