题目内容
10.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,A、B、C三点均在小正方形的顶点上.
(1)在图1中画出凸四边形ABCD,点D在小正方形的顶点上,且使四边形ABCD是只有一条对称轴的轴对称图形;
(2)在图2中画出凸四边形ABCE,点E在小正方形的顶点上,且使四边形ABCE是四条对称轴的轴对称图形.
分析 (1)根据轴对称图形的性质作出只有一条对称轴的图形即可求解;
(2)作出正方形ABCE即为所求四边形ABCE是四条对称轴的轴对称图形.
解答 解:(1)下面两个图形画出一个即可.
(2)如图所示:
点评 此题主要考查了轴对称图形的性质,作轴对称后的图形的依据是轴对称的性质,基本作法是:①先确定图形的关键点;②利用轴对称性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.

练习册系列答案
相关题目
20. 如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
①AC⊥BD ②BA⊥AD ③AB=BC ④AC=BD.
 如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
如图,下列选项中能使平行四边形ABCD是菱形的条件有( )①AC⊥BD ②BA⊥AD ③AB=BC ④AC=BD.
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
5.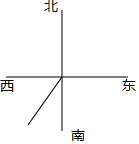 如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
 如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )| A. | 南偏东40°方向 | B. | 北偏西50°方向 | C. | 南偏东50°方向 | D. | 东南方向 |
17.$\sqrt{a^2}$=( )
| A. | a | B. | -a | C. | ${({\sqrt{a}})^2}$ | D. | |a| |
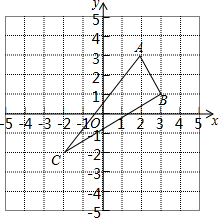 △ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(-2,-2)三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(-2,-2)三点在格点上. 在数学课上,老师请同学思考如下问题:
在数学课上,老师请同学思考如下问题: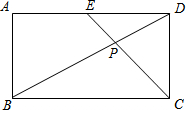 学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:
学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:
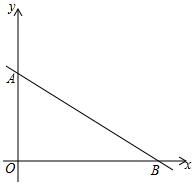 如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.