题目内容
在Rt△ABC中,∠C=90°,AB=10,BC=8,那么它的内切圆的半径为 .
考点:三角形的内切圆与内心
专题:
分析:首先设△ABC的内切圆半径为r,由在RT△ABC中,∠C=90°,AB=10,BC=8,可求得AC的长,又由S△ABC=
AC•BC=
r•(AC+BC+AB),即可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设△ABC的内切圆半径为r,
∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AC=
=6,
∴S△ABC=
AC•BC=
r•(AC+BC+AB),
∴r=
=
=2.
故答案为:2.
∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AC=
| AB2-BC2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| AC×BC |
| AC+BC+AB |
| 6×8 |
| 6+8+10 |
故答案为:2.
点评:此题考查了三角形的内切圆的性质.此题难度不大,注意掌握方程思想的应用.

练习册系列答案
相关题目
在“足球进校园”活动中规定:胜一场得3分,平一场得1分,负一场得0分.某班足球队踢了10场球,负了3场,得17分,这个足球队共胜了( )
| A、2场 | B、4场 | C、5场 | D、7场 |
 如图,△ABC和△A′B′C′关于MN对称,且AB=5,BC=3,则A′C′的取值范围是( )
如图,△ABC和△A′B′C′关于MN对称,且AB=5,BC=3,则A′C′的取值范围是( )| A、2<A′C′<8 |
| B、A′C′=8 |
| C、A′C′=5 |
| D、A′C′=2 |
 如图,AB⊥AC,且AB=AC,BN⊥AN,CM⊥AN,若BN=3,CM=5,则MN=
如图,AB⊥AC,且AB=AC,BN⊥AN,CM⊥AN,若BN=3,CM=5,则MN=
 如图,△ABC的面积为6
如图,△ABC的面积为6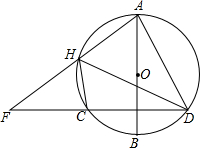 已知AB是⊙O的直径,弦CD⊥AB于点E,H是
已知AB是⊙O的直径,弦CD⊥AB于点E,H是
 已知:如图,点C,D在△ABE的边BE上,∠B=∠E,BC=ED,求证:AC=AD.
已知:如图,点C,D在△ABE的边BE上,∠B=∠E,BC=ED,求证:AC=AD. 如图,将一副三角板的直角顶点重合,若∠AOD=50°,则∠COB=
如图,将一副三角板的直角顶点重合,若∠AOD=50°,则∠COB=