题目内容
△ABC中,AC=8,BC边上的中线AD=6,则边AB的取值范围是 .
考点:三角形三边关系,全等三角形的判定与性质
专题:
分析:首先利用三角形的三边关系得到BC边一半的取值范围,然后得到BC的取值范围,然后利用三角形的三边关系得到AB的取值范围即可.
解答:解:∵AC=8,BC边上的中线AD=6,
∴线段CD的取值范围为8-6<BD<8+6,即:2<BD<14,
∴BC的取值范围为4<BD<28,
∵AC=8,
∴AB边的取值范围为:4<BD<20,
故答案为:4<BD<20.
∴线段CD的取值范围为8-6<BD<8+6,即:2<BD<14,
∴BC的取值范围为4<BD<28,
∵AC=8,
∴AB边的取值范围为:4<BD<20,
故答案为:4<BD<20.
点评:本题考查了三角形的三边关系,解题的关键是牢记三角形的三边关系,难度不大.

练习册系列答案
相关题目
已知矩形的对角线长为1,两条相邻的边长之和为m,则矩形的面积为( )
| A、m2+1 | ||
| B、m2-1 | ||
C、
| ||
D、
|
下列命题中假命题是( )
| A、对角线互相平分的四边形是平行四边形 |
| B、等腰梯形的对角线相等 |
| C、对角线相等的四边形是矩形 |
| D、顺次连接矩形各边中点,所得四边形为菱形 |
 如图,ABCD是正方形纸片,沿过点A的折痕将角D翻折,使得点D落在AC上的点D′处,则∠AED′=
如图,ABCD是正方形纸片,沿过点A的折痕将角D翻折,使得点D落在AC上的点D′处,则∠AED′=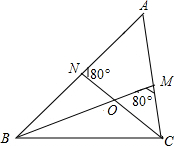 如图,点O是△ABC两条内角平分线BM、CN的交点,若∠ANC=∠BMC=80°,则∠A=
如图,点O是△ABC两条内角平分线BM、CN的交点,若∠ANC=∠BMC=80°,则∠A=