题目内容
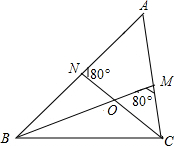 如图,点O是△ABC两条内角平分线BM、CN的交点,若∠ANC=∠BMC=80°,则∠A=
如图,点O是△ABC两条内角平分线BM、CN的交点,若∠ANC=∠BMC=80°,则∠A=考点:三角形内角和定理
专题:
分析:由角平分线的性质和三角形的内角和得到∠OBC=
∠ABC,∠OCB=
∠ACB,∠BOC=180°-∠OBC-∠OCB=90°+
∠A,进一步由四边形的内角和得出∠A+∠MON=180°,代换求得答案即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵BM、CN是角平分线,
∴∠OBC=
∠ABC,∠OCB=
∠ACB
在三角形BOC中,
∠BOC=180°-∠OBC-∠OCB
=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=90°+
∠A,
∴∠MON=∠BOC=90°+
∠A,
∵∠ANC=∠BMC=80°
∴∠OMA=100°
在四边形ANOM中
∠A+∠MON+∠ANC+∠BMC=180°
∴∠A+∠MON=180°
即∠A+90°+
∠A=180°
∴∠A=60°.
故答案为:60°.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
在三角形BOC中,
∠BOC=180°-∠OBC-∠OCB
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
∴∠MON=∠BOC=90°+
| 1 |
| 2 |
∵∠ANC=∠BMC=80°
∴∠OMA=100°
在四边形ANOM中
∠A+∠MON+∠ANC+∠BMC=180°
∴∠A+∠MON=180°
即∠A+90°+
| 1 |
| 2 |
∴∠A=60°.
故答案为:60°.
点评:此题考查三角形的内角和定理,角平分线的性质,四边形的内角和等知识点,结合图形,选择适当的方法解决问题.

练习册系列答案
相关题目
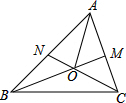 如图,点O是△ABC两条内角平分线BM、CN的交点,下列判断错误的是( )
如图,点O是△ABC两条内角平分线BM、CN的交点,下列判断错误的是( )| A、点O到△ABC三边距离相等 | ||
B、∠OBC+∠OCB=
| ||
| C、∠BOC-∠OAC=90° | ||
| D、∠BNC一定是钝角 |
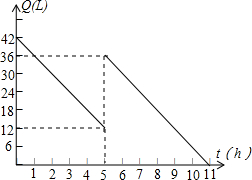 某机动车出发前油箱内有油42L,以40km/h匀速行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.
某机动车出发前油箱内有油42L,以40km/h匀速行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.