题目内容
8.计算:(1)$\sqrt{32}$-5$\sqrt{\frac{1}{2}}$+$\frac{6}{{\sqrt{8}}}$
(2)$\sqrt{12}$×$\sqrt{\frac{1}{3}}$-${(2-\sqrt{3})^2}$(2+$\sqrt{3}$).
分析 (1)先化简二次根式,再合并同类二次根式即可;
(2)根据二次根式的乘法、平方差公式进行计算即可.
解答 解:(1)原式=4$\sqrt{2}$-$\frac{5\sqrt{2}}{2}$+$\frac{3\sqrt{2}}{2}$
=3$\sqrt{2}$;
(2)原式=2-(2-$\sqrt{3}$)
=2-2+$\sqrt{3}$
=$\sqrt{3}$.
点评 本题考查了二次根式的混合运算,掌握二次根式的乘法、合并同类二次根式和平方差公式是解题的关键.

练习册系列答案
相关题目
19.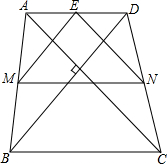 如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )
如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )
 如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )
如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 不能确定 |
16.已知x=3是方程x2-2x+a=0的根,则a等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
13.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (-3pq)2=-6p2q2 | C. | (-bc)4÷(-bc)2=b2c2 | D. | a+a=a2 |
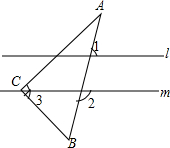 如图,一块含30°角的直角三角板ABC (∠C=90°,∠A=30°)的直角顶点C放置在直线m上,且l∥m,∠1=70°,则∠2=110°,∠3=50°.
如图,一块含30°角的直角三角板ABC (∠C=90°,∠A=30°)的直角顶点C放置在直线m上,且l∥m,∠1=70°,则∠2=110°,∠3=50°.