Question

在△ABC中，角平分线AD与BC交于D，AB=c，BC=a，CA=b，求BD、CD之长度（用a、b、c表示）．

Answer 1

考点：角平分线的性质

专题：

分析：作DE∥AC，得出∠EDA=∠DAC，由于AD是∠BAC的平分线，得出∠BAD=∠DAC，进而得出∠EAD=∠EDA，根据等角对等边得出EA=ED，设DE=x，则EA=x，BE=c-x，然后根据△BDE∽△BCA对应边成比例，得出

BD

BC

=

BE

AB

=

DE

AC

，即可求得BD的值，最后根据CD=BC-BD求得CD的值．

解答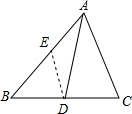：解：作DE∥AC，
∴∠EDA=∠DAC，
∵AD是∠BAC的平分线，
∴∠BAD=∠DAC，
∴∠EAD=∠EDA，
∴EA=ED，
∵DE∥AC，
∴△BDE∽△BCA，
∴

BD

BC

=

BE

AB

=

DE

AC

设DE=x，则EA=x，
∴BE=c-x，
∴

BD

a

=

c-x

c

=

x

b

，
∴x=

bc

b+c

，BD=a（1-

x

c

），
∴BD=a（1-

bc b+c

c

）=

ac

b+c

，
∴CD=BC-BD=a-

ac

b+c

=

ab

b+c

．

点评：本题考查了角平分线的性质，平行线的性质，相似三角形的判定和性质，作出辅助线，得出DE=AE是本题的关键．