题目内容
 如图,两同心圆半径分别为15、20,大圆的弦AD与小圆交于BC,若CD=7,点O为两圆的圆心,则O点到AD的距离等于
如图,两同心圆半径分别为15、20,大圆的弦AD与小圆交于BC,若CD=7,点O为两圆的圆心,则O点到AD的距离等于考点:垂径定理,勾股定理
专题:计算题
分析:作OH⊥BC于H,连结OC、OD,根据勾股定理得到OH2+(HC+7)2=202,OH2+HC2=152,然后利用加减消元法可求出OH.
解答: 解:作OH⊥BC于H,连结OC、OD,如图,
解:作OH⊥BC于H,连结OC、OD,如图,
则HD=HC+CD=HC+7,
在Rt△ODH中,OH2+HD2=OD2,即OH2+(HC+7)2=202①,
在Rt△OCH中,OH2+HC2=OC2,即OH2+HC2=152②,
①-②得14HC+49=400-225,解得HC=9,
把HC=9代入②得OH2+92=152,解得OH=12,
所以O点到AD的距离为12.
故答案为12.
 解:作OH⊥BC于H,连结OC、OD,如图,
解:作OH⊥BC于H,连结OC、OD,如图,则HD=HC+CD=HC+7,
在Rt△ODH中,OH2+HD2=OD2,即OH2+(HC+7)2=202①,
在Rt△OCH中,OH2+HC2=OC2,即OH2+HC2=152②,
①-②得14HC+49=400-225,解得HC=9,
把HC=9代入②得OH2+92=152,解得OH=12,
所以O点到AD的距离为12.
故答案为12.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目
在频数分布直方图中,各个小长方形的高( )
| A、与频数成正比 |
| B、与频数成反比 |
| C、与频数不成正比也不成反比 |
| D、与频数无关 |
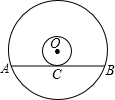 如图所示是一张电脑光盘的表面,两个圆的圆心是点O,大圆的弦AB所在直线是小圆的切线,弦AB=4
如图所示是一张电脑光盘的表面,两个圆的圆心是点O,大圆的弦AB所在直线是小圆的切线,弦AB=4