题目内容
12．
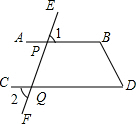如图，已知∠1=∠2，∠D=55°，求∠B的度数．
分析 先由对顶角相等，可得：∠2=∠EQD，然后由∠1=∠2，可得：∠1=∠EQD，然后根据同位角相等两直线平行，可得：AB∥CD，然后根据两直线平行同旁内角互补，可得：∠B+∠D=180°，然后由∠D=55°，进而可求∠B的度数．
解答 证明：∵∠1=∠2，∠2=∠EQD，
∴∠1=∠EQD，
∴AB∥CD，
∴∠B+∠D=180°，
∵∠D=55°，
∴∠B=125°．
点评 此题考查了平行线的判定与性质，熟记同位角相等?两直线平行；内错角相等?两直线平行；同旁内角互补?两直线平行．是解题的关键．
练习册系列答案
相关题目
2．
如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，直角∠MON的顶点O在AB边上，OM、ON分别交边AC、BC于点P、Q，∠MON绕点O任意旋转．当$\frac{OA}{OB}=\frac{1}{2}$时，$\frac{OP}{OQ}$的值为 ______；当$\frac{OA}{OB}=\frac{1}{n}$时，$\frac{OP}{OQ}$的值为 ______（用含n的式子表示）．其中正确的选项是（ ）
如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，直角∠MON的顶点O在AB边上，OM、ON分别交边AC、BC于点P、Q，∠MON绕点O任意旋转．当$\frac{OA}{OB}=\frac{1}{2}$时，$\frac{OP}{OQ}$的值为 ______；当$\frac{OA}{OB}=\frac{1}{n}$时，$\frac{OP}{OQ}$的值为 ______（用含n的式子表示）．其中正确的选项是（ ）| A． | $\frac{\sqrt{3}}{2}；\frac{\sqrt{3}}{n}$ | B． | $\frac{\sqrt{3}}{n}；\frac{\sqrt{3}}{n}$ | C． | $\frac{\sqrt{3}}{2}；\sqrt{3}$ | D． | $\sqrt{3}$；$\frac{\sqrt{3}}{n}$ |
20．顺次连接矩形的四边形中点所得的四边形一定是（ ）
| A． | 平行四边形 | B． | 矩形 | C． | 菱形 | D． | 正方形 |
作图题
17．已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
| A． | 当AB=BC时，四边形ABCD是菱形 | B． | 当AC=BD时，四边形是正方形 | ||
| C． | 当∠ABC=90°时，四边形是矩形 | D． | 当AC⊥BD时，四边形是菱形 |
1．已知一个多边形的内角和是540°，则这个多边形是（ ）
| A． | 五边形 | B． | 四边形 | C． | 六边形 | D． | 七边形 |