题目内容
20．在△ABC中，∠C=90°，AB=5，BC=3，则sinB=$\frac{4}{5}$．分析 根据勾股定理求出AC，根据正弦的定义计算即可．
解答 解：∵∠C=90°，AB=5，BC=3，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4，
∴sinB=$\frac{AC}{AB}$=$\frac{4}{5}$．
故答案为：$\frac{4}{5}$．
点评 本题考查的是锐角三角函数的定义，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
相关题目
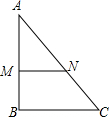如图，在△ABC中，AC=10，AB=8，直线l分别与AB，AC交于M，N两点，且l∥BC，若S△AMN：S△ABC=4：9，则AM+AN的长为（ ）
请你根据王老师所给的内容，完成下列各小题．
如图，在平行四边形ABCD中，AB=5，BC=8，∠ABC的角平分线交AD于E，F在AE上，且AF=3，BE与CF交于点G，则△EFG与△BCG面积之比是$\frac{1}{16}$．
5．一组数据如下：3，6，7，2，3，4，3，6，那么这组数据的中位数和众数分别是（ ）
| A． | 3，3 | B． | 3.5，3 | C． | 4，3 | D． | 3.5，6 |