题目内容
已知某三角形三边分别是m2-n2、2mn、m2+n2（m＞n），且m、n都是整数，此三角形是（ ）
| A、直角三角形 |
| B、等腰直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
考点：勾股定理的逆定理
专题：
分析：根据勾股定理的逆定理可得到该三角形是直角三角形．
解答：解：∵某三角形三边分别是m2-n2、2mn、m2+n2（m＞n），且m、n都是整数，
∴（m2-n2）2+（2mn）2=m4+n4+2（mn）2=（m2+n2）2，
∴此三角形是直角三角形．
故选A．
∴（m2-n2）2+（2mn）2=m4+n4+2（mn）2=（m2+n2）2，
∴此三角形是直角三角形．
故选A．
点评：本题考查了勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
练习册系列答案
春雨教育同步作文系列答案
相关题目
如图，已知AD平分∠BAC交BC于D，CE⊥AD于E，∠B=26°，∠DCE=34°，则∠BAC的度数为一个袋中装有红、黄、白球各2个，为了确保一次从中取出的球3种颜色都有，则最小要取出（ ）
| A、6个球 | B、5个球 |
| C、4个球 | D、3个球 |
如图是一个风景区，A，B，C，D，E，F是这一风景区内的五个主要景点，现观光者聚于A点．假若你是导游，要带领游客欣赏这五个景点后再回到A点，但又不想多走“冤枉路”（不能走重复的路线和经过同一个景点），你认为可选择行走路线有（ ）种．| A、4 | B、5 | C、6 | D、7 |
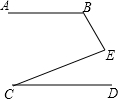如图，若AB∥CD，则∠B、∠C、∠E三者之间的关系是（ ）| A、∠B+∠C+∠E=180° |
| B、∠B+∠E-∠C=180° |
| C、∠B+∠C-∠E=180° |
| D、∠C+∠E-∠B=180° |
已知甲乙两个样本，如果甲的样本方差为0.4，乙的样本方差为0.6，那么（ ）
| A、甲的波动比乙的大 |
| B、乙的波动比甲的大 |
| C、甲、乙波动一样大 |
| D、无法确定 |
如图，四边形ABCD是正方形，直线L1、L2、L3，若L1与L2的距离为5，L2与L3的距离为7，则正方形ABCD的面积等于（ ）| A、70 | B、74 |
| C、144 | D、148 |