题目内容
5.(1)对于a,b定义一种新运算“☆”:a☆b=2a-b,例如:5☆3=2×5-3=7.若(x☆5)<-2,求x的取值范围;(2)先化简再求值:$\frac{{{x^2}-2x}}{{{x^2}-4x+4}}$÷$\frac{x}{{x}^{2}-4}$,其中x的值是(1)中的正整数解.
分析 (1)先根据题意得出关于x的不等式,求出x的取值范围即可;
(2)先根据分式混合运算的法则把原式进行化简,再根据(1)中x的取值范围得出x的整数解,把x的值代入进行计算即可.
解答 (1)解:∵a☆b=2a-b,
∴x☆5=2x-5,
∴(x☆5)<-2可化为2x-5<-2,解得x<$\frac{3}{2}$;
(2)解:原式=$\frac{x(x-2)}{{{{(x-2)}^2}}}•\frac{(x+2)(x-2)}{x}$
=x+2,
∵x<$\frac{3}{2}$且x为正整数解,
∴x=1,
∴当x=1时,原式=x+2=3.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
15.2015年1月20日,参加成都市第十六届人大第三次会议的代表审查了《2015年财政预算草案的报告》,报告显示,2015年教育预算支出为661000万元,数据“661000”用科学记数法表示为( )
| A. | 6.61×105 | B. | 6.61×106 | C. | 66.1×104 | D. | 0.661×106 |
20.若实数x,y满足|x-4|+$\sqrt{y-8}$=0,则以x,y的值为两边长的等腰三角形的周长是( )
| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
14.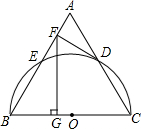 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )| A. | 4 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
15.在运动会上,成绩是按点到直线的距离来评定的有( )
| A. | 跳远 | B. | 跳高 | C. | 掷铅球 | D. | 掷标枪 |
 一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )
一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )