题目内容
15.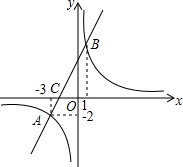 如图,一次函数y=kx+b图象与反比例函数y=$\frac{m}{x}$的图象交于点A、B,与x轴交于点C.
如图,一次函数y=kx+b图象与反比例函数y=$\frac{m}{x}$的图象交于点A、B,与x轴交于点C.(1)求一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的解析式.
(2)求点C坐标.
(3)平面上的点D与点O、C、A构成平行四边形,请直接写出满足条件的D点坐标(-5,-2)或(-1,-2)或(1,2).
分析 (1)把A坐标代入反比例解析式求出m的值,再将x=1代入反比例解析式求出y的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)对于一次函数y=kx+b,令y=0求出x的值,确定出C坐标即可;
(3)如图所示,分三种情况考虑:利用平行四边形的性质确定出D坐标即可.
解答 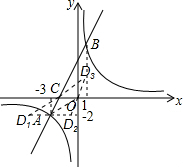 解:(1)把A(-3,-2)代入y=$\frac{m}{x}$得:m=6,
解:(1)把A(-3,-2)代入y=$\frac{m}{x}$得:m=6,
把B横坐标x=1代入y=$\frac{6}{x}$得:y=6,即B(1,6),
把(-3,-2),(1,6)代入y=kx+b得:$\left\{\begin{array}{l}{-3k+b=-2}\\{k+b=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$,
∴一次函数解析式为y=2x+4;
(2)对于y=2x+4,
令y=0,得到x=-2,
则C的坐标为(-2,0);
(3)如图所示,分三种情况考虑:
根据题意得:D1(-5,-2);D2(-1,-2);D3(1,2).
故答案为:(-5,-2)或(-1,-2)或(1,2)
点评 此题属于反比例函数解析式,涉及的知识有:待定系数法确定函数解析式,坐标与图形性质,一次函数与坐标轴的交点,以及平行四边形的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
5.2012伦敦奥运会主会场的座席数是91000个,这个数用科学记数法表示为( )
| A. | 0.91×105 | B. | 9.1×104 | C. | 91×103 | D. | 9.1×103 |
3.邗江区青少年活动中心组织一次少年跳绳比赛,各年龄组的参赛人数如下表所示:
则全体参赛选手年龄的中位数是13.5岁.
| 年龄组 | 12岁 | 13岁 | 14岁 | 15岁 |
| 参赛人数 | 5 | 20 | 12 | 13 |
10.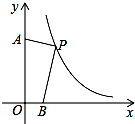 已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )
已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )
 已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )
已知P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,点B的坐标为(5,0),A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,那么四边形AOBP的面积为( )| A. | 16 | B. | 20 | C. | 24 | D. | 28 |
20.若实数x,y满足|x-4|+$\sqrt{y-8}$=0,则以x,y的值为两边长的等腰三角形的周长是( )
| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
7.下列运算正确的是( )
| A. | 3a2-a2=3 | B. | (a2)3=a5 | C. | a3•a6=a9 | D. | a6÷a3=a2 |

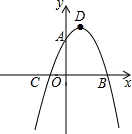 如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.
如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.