题目内容
7. 如图,BD=CE,求证:AC•EF=AB•DF.
如图,BD=CE,求证:AC•EF=AB•DF.
分析 作出EM∥AB,构造出△ABC∽△EMC,△DBF∽△EMF,根据相似三角形的性质,即可得出结论.
解答 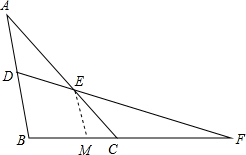 证明:过点E作EM∥AB交BF于M,如图
证明:过点E作EM∥AB交BF于M,如图
∵EM∥AB,
∴△ABC∽△EMC,
∴$\frac{AB}{EM}=\frac{AC}{CE}$,
即$\frac{AC}{AB}=\frac{CE}{EM}$,
∵BD∥EM,
∴△DBF∽△EMF,
∴$\frac{DF}{EF}=\frac{DB}{EM}$,
∵BD=CE,
∴$\frac{DF}{EF}=\frac{CE}{EM}$,
∴$\frac{AC}{AB}=\frac{DF}{EF}$,
即AC•EF=AB•DF.
点评 本题考查了相似三角形的判断和性质,此题构思极其巧妙,考查了同学们的创造性思维能力.解答此题的关键作出辅助线,建立起各线段之间的联系.

练习册系列答案
相关题目
16.人体内成熟的红细胞的平均直径为0.0000077米,用科学记数法表示为( )
| A. | 0.77×10-7 | B. | 7.7×10-7 | C. | 0.77×10-6 | D. | 7.7×10-6 |
 某校期中考试后,为了更好地了解七年级测试的数学成绩情况,随机抽取了部分学生的试卷.对学生的数学成绩(得分取整数)进行赘理.分成五组,并绘制成如下不完整的频数分布直方图.在直方图中从左到右依次为一、二、三、四、五组.成绩没有低于20分的,第五组的人数占抽样人数的30%.第四组的人数是第二组的人数的4倍.请结合信息回答下列问题.
某校期中考试后,为了更好地了解七年级测试的数学成绩情况,随机抽取了部分学生的试卷.对学生的数学成绩(得分取整数)进行赘理.分成五组,并绘制成如下不完整的频数分布直方图.在直方图中从左到右依次为一、二、三、四、五组.成绩没有低于20分的,第五组的人数占抽样人数的30%.第四组的人数是第二组的人数的4倍.请结合信息回答下列问题.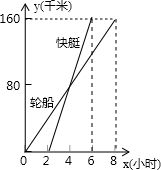 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;
如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;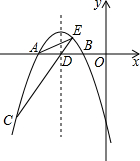 如图,抛物线y=-$\frac{1}{2}$x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(-6,0),点C的坐标是(-8,-6).
如图,抛物线y=-$\frac{1}{2}$x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(-6,0),点C的坐标是(-8,-6).