题目内容
5.已知x、y为正数,且|x2-4|+(y2-3)2=0,如果以x,y的长为直角边作一直角三角形,那么以此直角三角形的斜边为边长的正方形的面积为7.分析 根据x与y为正数,由已知等式,利用非负数的性质及算术平方根定义求出x与y的值,再利用勾股定理及正方形面积求法即可确定出所求.
解答 解:∵x、y为正数,且|x2-4|+(y2-3)2=0,
∴x2-4=0,y2-3=0,
解得:x=2,y=$\sqrt{3}$.
则以此直角三角形的斜边为边长的正方形的面积为x2+y2=4+3=7.
故答案为:7.
点评 此题考查了勾股定理,正方形的性质,以及非负数的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若一元二次方程ax2+bx+c=0中的二次项系数、一次项系数与常数项之和等于零,那么方程必有一个根是( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
20.?ABCD的对角线交于点O,下列结论错误的是( )
| A. | 平行四边形ABCD是中心对称图形 | B. | △ABC≌△COD | ||
| C. | △AOB≌△COD | D. | △AOB与△BOC的面积相等 |
15.若直线y=x-1与抛物线y=x2+5x+a2相交,则它们的交点一定在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
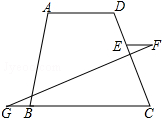 已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?
已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?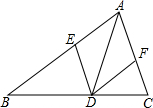 如图,已知AD平分∠BAC,要使△ADE≌△ADF,只需再添加一个条件就可以了,你选择的条件是AE=AF,理由是SAS.
如图,已知AD平分∠BAC,要使△ADE≌△ADF,只需再添加一个条件就可以了,你选择的条件是AE=AF,理由是SAS.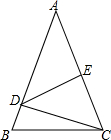 如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△BDC的周长为13cm,则△ABC的周长为19.
如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△BDC的周长为13cm,则△ABC的周长为19.