题目内容
17.已知:a=$\sqrt{2}$+$\sqrt{3}$,b=$\frac{1}{\sqrt{2}-\sqrt{3}}$,则a与b的关系为a>b.分析 把b进行分母有理化,再进行比较a与b的关系.
解答 解:b=$\frac{1}{\sqrt{2}-\sqrt{3}}=\frac{\sqrt{2}+\sqrt{3}}{(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})}$=$\frac{\sqrt{2}+\sqrt{3}}{2-3}=-(\sqrt{2}+\sqrt{3})$,
∵$\sqrt{2}+\sqrt{3}>-(\sqrt{2}+\sqrt{3})$,
∴a>b,
故答案为:a>b.
点评 本题考查了分母有理化,解决本题的关键是先把b进行分母有理化,再进行比较大小.

练习册系列答案
相关题目
7.下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )
| A. | a=3,b=4,c=5 | B. | a=5,b=12,c=13 | ||
| C. | a=1,b=3,c=$\sqrt{10}$ | D. | a=$1\frac{3}{7}$,b=$1\frac{4}{7}$,c=$1\frac{5}{7}$ |
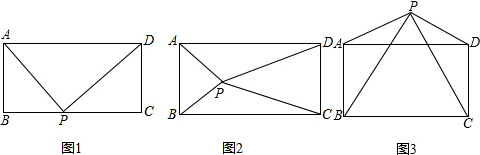
 已知△ABC,求作:点P,使PA=PB,且点P到∠A的两边距离相等.
已知△ABC,求作:点P,使PA=PB,且点P到∠A的两边距离相等.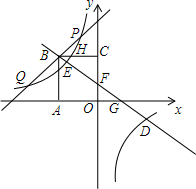 如图,正方形ABCO的顶点A,C分别在x轴,y轴上,O为坐标原点,点B在第二象限,边长为m,双曲线线y=$\frac{k}{x}$(x≠0)经过BC的中点H.
如图,正方形ABCO的顶点A,C分别在x轴,y轴上,O为坐标原点,点B在第二象限,边长为m,双曲线线y=$\frac{k}{x}$(x≠0)经过BC的中点H.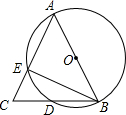 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的个数是( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的个数是( )
 在图中作出点P,使得点P到C、D两点的距离相等,并且点P到OA、OB的距离也相等.(用尺规作图,保留作图痕迹,不写作法.)
在图中作出点P,使得点P到C、D两点的距离相等,并且点P到OA、OB的距离也相等.(用尺规作图,保留作图痕迹,不写作法.)