题目内容
14.如图1,平面直角坐标系xOy中,抛物线y=$\frac{4}{3}$x2+bx-4与x轴交于A、B两点(点B在点A右侧),与y轴交于点C,点B的坐标为(1,0),抛物线上有一动点P,点P的横坐标为m,且-3<m<0,过点P作y轴的平行线分别交x轴和直线AC于点D和E.(1)求抛物线及直线AC的函数关系式.
(2)连接PC,求出当△PEC是直角三角形时m的值.
(3)如图2,连接BC,则在第二象限内是否存在一点M,使得四边形PCBM是矩形?如果存在,直接写出此时点P和点M的坐标;如果不存在,请说明理由.

分析 (1)把B点坐标代入y=$\frac{4}{3}$x2+bx-4中求出b即可得到抛物线的解析式,则利用解方程$\frac{4}{3}$x2+$\frac{8}{3}$x-4=0得A(-3,0),再确定C点坐标,然后利用待定系数法求直线AC的解析式;
(2)如图1,讨论:当∠EPC=90°时,PC∥x轴,则点P与点C为抛物线上的对称点,利用抛物线的对称性可确定此时P点坐标,从而得到此时m的值;当∠ECP=90°,则EC⊥PC,根据来那个直线垂直,一次项系数互为负倒数得到直线PC的解析式为y=$\frac{3}{4}$x-4,然后通过解方程组$\left\{\begin{array}{l}{y=\frac{4}{3}{x}^{2}+\frac{8}{3}x-4}\\{y=\frac{3}{4}x-4}\end{array}\right.$得P点坐标,从而得到即此时m的值;
(3)如图2,先利用待定系数法求出直线BC的解析式为y=4x-4,再根据PC⊥BC得到直线PC的解析式为y=-$\frac{1}{4}$x-4,于是解方程组$\left\{\begin{array}{l}{y=\frac{4}{3}{x}^{2}+\frac{8}{3}x-4}\\{y=-\frac{1}{4}x-4}\end{array}\right.$得P点坐标,然后利用点C平移到点P的规律,写出点B平移到点M的规律,从而得到M点坐标.
解答 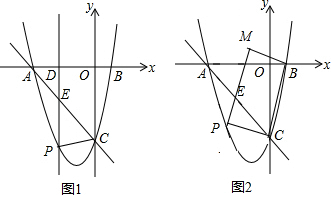 解:(1)把B(1,0)代入y=$\frac{4}{3}$x2+bx-4得$\frac{4}{3}$+b-4=0,解得b=$\frac{8}{3}$,
解:(1)把B(1,0)代入y=$\frac{4}{3}$x2+bx-4得$\frac{4}{3}$+b-4=0,解得b=$\frac{8}{3}$,
∴抛物线的解析式为y=$\frac{4}{3}$x2+$\frac{8}{3}$x-4,
当y=0时,$\frac{4}{3}$x2+$\frac{8}{3}$x-4=0,解得x1=-3,x2=1,则A(-3,0),
当x=0时,y=$\frac{4}{3}$x2+$\frac{8}{3}$x-4=-4,则C(0,-4),
设直线AC的解析式为y=kx+n,
把A(-3,0),C(0,4)代入得$\left\{\begin{array}{l}{-3k+n=0}\\{n=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{n=-4}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{4}{3}$x-4;
(2)如图1,
当∠EPC=90°时,PC∥x轴,则点P与点C为抛物线上的对称点,而抛物线的对称轴为直线x=-1,所以此时P点坐标为(-2,-4),即此时m的值为-2;
当∠ECP=90°,则EC⊥PC,所以直线PC的解析式为y=$\frac{3}{4}$x-4,
解方程组$\left\{\begin{array}{l}{y=\frac{4}{3}{x}^{2}+\frac{8}{3}x-4}\\{y=\frac{3}{4}x-4}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{23}{16}}\\{y=-\frac{325}{64}}\end{array}\right.$,所以P(-$\frac{23}{16}$,-$\frac{325}{64}$),即此时m的值为-$\frac{23}{16}$,
综上所述,m的值为-2或-$\frac{23}{16}$;
(3)存在.
如图2,设直线BC的解析式为y=px+q,
把B(1,0),C(0,-4)代入得$\left\{\begin{array}{l}{p+q=0}\\{q=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=4}\\{q=-4}\end{array}\right.$,
∴直线BC的解析式为y=4x-4,
∵四边形PCBM为矩形,
∴∠PCB=90°,即PC⊥BC,
∴直线PC的解析式为y=-$\frac{1}{4}$x-4,
解方程组$\left\{\begin{array}{l}{y=\frac{4}{3}{x}^{2}+\frac{8}{3}x-4}\\{y=-\frac{1}{4}x-4}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{35}{16}}\\{y=-\frac{221}{64}}\end{array}\right.$,所以P(-$\frac{35}{16}$,-$\frac{221}{64}$),
∵点C向右平移$\frac{35}{16}$个单位,再向上平移$\frac{35}{64}$个单位得到点P,
∴点B向右平移$\frac{35}{16}$个单位,再向上平移$\frac{35}{64}$个单位得到点M,
∴M(-$\frac{19}{16}$,$\frac{35}{64}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和矩形的性质;会利用待定系数法求抛物线和一次函数解析式,会把求两个函数的交点坐标问题转化为解方程组的问题,理解垂直两直线的一次项系数的负倒数关系;理解坐标与图形性质,掌握点平移的坐标规律;会运用分类讨论的思想解决数学问题.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | $\sqrt{3}$+$\sqrt{4}$=$\sqrt{7}$ | B. | 3$\sqrt{5}$-$\sqrt{5}$=3 | C. | $\sqrt{2}$×$\sqrt{5}$=10 | D. | $\sqrt{18}$÷$\sqrt{2}$=3 |
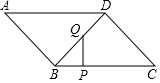 如图,在?ABCD中,BC=20$\sqrt{2}$cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为3$\sqrt{2}$cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
如图,在?ABCD中,BC=20$\sqrt{2}$cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为3$\sqrt{2}$cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )| A. | 4s | B. | $\frac{5}{2}$s | C. | $\frac{5}{2}$s或4s | D. | 6s |
 如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠AOF=25°,求∠CDO的度数( )
如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠AOF=25°,求∠CDO的度数( )| A. | 50° | B. | 45° | C. | 35° | D. | 65° |
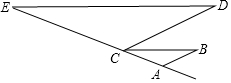 已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA
已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA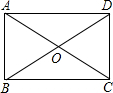 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=1,则AD的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=1,则AD的长为$\sqrt{3}$.