题目内容
已知平面直角坐标系中的两点A(2,4),B(11,13),P为x轴上一动点,求使得PB-PA最大时点P点坐标.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:由三角形两边之差小于第三边可知,当A、B、P三点不共线时,|PA-PB|<AB,又因为A(2,4),B(11,13)两点都在x轴同侧,则当A、B、P三点共线时,|PA-PB|=AB,即|PA-PB|≤AB,所以本题中当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.先运用待定系数法求出直线AB的解析式,再令y=0,求出x的值即可.
解答: 解:由题意可知,当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.
解:由题意可知,当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.
设直线AB的解析式为y=kx+b,
∵A(2,4),B(11,13),
∴
,
解得
.
∴y=x+2,
令y=0,得0=x+2,
解得x=-2.
∴点P的坐标是(-2,0).
 解:由题意可知,当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.
解:由题意可知,当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.设直线AB的解析式为y=kx+b,
∵A(2,4),B(11,13),
∴
|
解得
|
∴y=x+2,
令y=0,得0=x+2,
解得x=-2.
∴点P的坐标是(-2,0).
点评:本题考查了三角形的三边关系定理,运用待定系数法求一次函数的解析式及x轴上点的坐标特征,难度适中.根据三角形两边之差小于第三边得出当点P在直线AB上时,P点到A、B两点距离之差的绝对值最大,是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
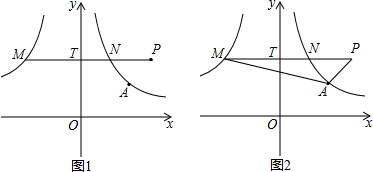
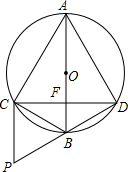 若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=
若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=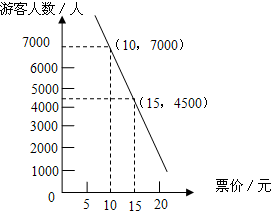 某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?
某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?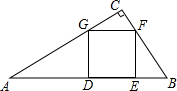 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.