Question

18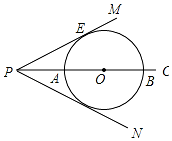．如图，已知PC平分∠MPN，点O是PC上任意一点，PM与⊙O相切于点E，交PC于A、B两点．
（1）求证：PN与⊙O相切；
（2）如果∠MPC=30°，PE=2$\sqrt{3}$，求⊙O的半径．

Answer 1

分析 （1）连接OE，过O作OF⊥PN，如图所示，利用AAS得到三角形PEO与三角形PFO全等，利用全等三角形对应边相等得到=OE，即可确定出PN与圆O相切；
（2）在直角三角形POE中，利用30度角的正切值求出OE的长，即⊙O的半径的长度．

解答 解：
（1）证明：连接OE，过O作OF⊥PN，如图所示，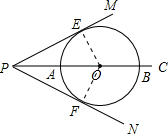
∵PM与圆O相切，
∴OE⊥PM，
∴∠OEP=∠OFP=90°，
∵PC平分∠MPN，
∴∠EPO=∠FPO，
在△PEO和△PFO中，
$\left\{\begin{array}{l}{∠EPO=∠FPO}\\{∠OEP=∠OFP}\\{OP=OP}\end{array}\right.$，
∴△PEO≌△PFO（AAS），
∴OF=OE，
即PN与圆O相切；
（2）在Rt△EPO中，∠MPC=30°，PE=2$\sqrt{3}$，
∴tan30°=$\frac{OE}{PE}$=$\frac{\sqrt{3}}{3}$，
∴OE=2．

点评 此题考查了切线的判定与性质，全等三角形的判断和性质以及特殊角的锐角三角函数值，熟练掌握切线的判定与性质是解本题的关键．