题目内容
18. 在△ABC中,∠ACB=90°,BA=5,AC=3,如图,以AB所在直线为x轴,以AB的垂直平分线为y轴,建立直角坐标系,求点A、B、C的坐标.
在△ABC中,∠ACB=90°,BA=5,AC=3,如图,以AB所在直线为x轴,以AB的垂直平分线为y轴,建立直角坐标系,求点A、B、C的坐标.
分析 由AB=5,以AB的垂直平分线为y轴,从而可求得点A和点B的坐标,过点C作CD⊥AB,由三角形面积为定值可求出CE的长,再根据勾股定理求出AE的长,即可求得点C的坐标.
解答 解:如图所示:过点C作CD⊥AB,垂足为D.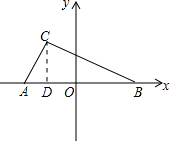
∵y轴是AB的垂直平分线,
∴OA=OB.
∵AB=5,
∴点A的坐标为(-2.5,0),点B的坐标为(2.5,0);
∵∠ACB=90°,BA=5,AC=3,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4,
∵AC•BC=CD•AB,
∴CD=$\frac{12}{5}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\frac{9}{5}$,
∴OD=AO-AD=$\frac{5}{2}$-$\frac{9}{5}$=$\frac{16}{5}$,
∴点C的坐标是(-$\frac{16}{5}$,$\frac{12}{5}$).
点评 本题考查了勾股定理的运用以及坐标与图形的性质,作斜边上的高,构造出直角三角形并利用性质是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
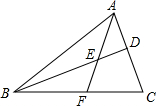 如图,在△ABC中,点D在AC上,点E在BD上,且$\frac{AD}{DC}$=$\frac{2}{3}$,$\frac{BE}{ED}$=$\frac{3}{2}$,AE的延长线交BC于点F,求BF:FC.
如图,在△ABC中,点D在AC上,点E在BD上,且$\frac{AD}{DC}$=$\frac{2}{3}$,$\frac{BE}{ED}$=$\frac{3}{2}$,AE的延长线交BC于点F,求BF:FC.