题目内容

4．代数式2x2+3x-1的最小值是（　　）
A．$-\frac{7}{4}$B．$-\frac{17}{8}$C．-2D．-3

分析 先利用配方法将代数式2x2+3x-1转化为完全平方与数字的形式，然后根据非负数的性质进行解答．

解答 解：2x2+3x-1
=2（x2+$\frac{3}{2}$x+$\frac{9}{16}$）-2×$\frac{9}{16}$-1
=2（x+$\frac{3}{4}$）2-$\frac{17}{8}$．
∵2（x+$\frac{3}{4}$）2≥0，
∴2x2+3x-1的最小值是-$\frac{17}{8}$．
故选：B．

点评 本题考查了配方法的应用．解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．

练习册系列答案
相关题目
14．-3-（2-4）=（　　）
A．-1B．-5C．-9D．1
15．在矩形纸片ABCD的正中间，摆放一个菱形EFGH，形成如图1所示的轴对称图形，已知AB=8，BC=16，∠E=60°．现将矩形纸片折叠，使矩形的顶点C与对角线交点O重合，折痕为MN，如图2所示，如果菱形的顶点G恰好落在折痕MN上，则菱形EFGH的面积为$\frac{50}{3}\sqrt{3}$．
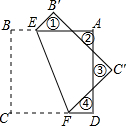12．如图，正方形纸片ABCD的边长为8，E、F分别为AB、CD边上的点，将纸片沿EF折叠，求图中①②③④四个三角形的周长之和．
19．阅读下列材料，然后解答后面的问题．
我们知道方程2x+3y=12有无数组解，但在实际生活中我们往往只需要求出其正整数解．
例：由2x+3y=12，得y=$\frac{12-2x}{3}$=4-$\frac{2}{3}$x，（x、y为正整数）
∴$\left\{\begin{array}{l}{x＞0}\\{\frac{12-x}{3}＞0}\end{array}\right.$ 则有0＜x＜6．又y=4-$\frac{2}{3}$x为正整数，则$\frac{2}{3}x$为正整数．
∴x为3的倍数，从而x=3，代入y=4-$\frac{2}{3}x$=2．
∴2x+3y=12的正整数解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$
问题：（1）请你写出方程2x+y=5的一组正整数解：
（2）若$\frac{6}{x-2}$为自然数，则满足条件的x值有C 个
A、2      B、3       C、4        D、5
（3）七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？
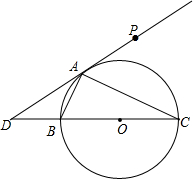9．如图所示，Rt△ABC中，∠BAC=90°，∠C=30°，BC=2，⊙O是△ABC的外接圆，D是CB延长线上一点，且BD=1，连接DA，点P是射线DA上的动点．
（1）求证DA是⊙O的切线；
（2）DP的长度为多少时，∠BPC的度数最大，最大度数是多少？请说明理由．
（3）P运动的过程中，（PB+PC）的值能否达到最小，若能，求出这个最小值，若不能，说明理由．
16．如图，已知A（m，3）是一次函数y=kx+b与反函数y=$\frac{6}{x}$（x＞0）的交点．
（1）求m的值；
（2）若一次函数分别与x、y轴交于E、F两点，A为EF的中点，试求该一次函数的解析式；
（3）在y=$\frac{6}{x}$的图象上另取一点B，作BK⊥x轴于K，在（2）的条件下，在y轴上取一点C，使得FO=4CO．问：在y轴上是否存在点P，使得△PAC和△PBK的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．
13．若抛物线L：y=ax2+bx+c（a，b，c是常数，a≠0）的顶点P在直线l上，则称该抛物线L与直线l具有“”一带一路关系，此时，抛物线L叫做直线l的“带线”，直线l叫做抛物线L的“路线”．
（1）求“带线”L：y=x2-2mx+m2+m-1（m是常数）的“路线”l的解析式；
（2）若某“带线”L：y=$\frac{1}{2}$x2+bx+c的顶点在二次函数y=x2+4x+1的图象上，它的“路线”l的解析式为y=2x+4．
①求此“带线”L的解析式；
②设“带线”L与“路线”l的另一个交点为Q，点R在PQ之间的“带线”L上，当点R到“路线”l的距离最大时，求点R的坐标．
14．已知实数x＞0，实数y满足式子y=3-$\sqrt{{x}^{2}-2}+\sqrt{2-{x}^{2}}$，则x2y=（　　）
A．0B．3C．6D．3$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网