题目内容
已知关于x的二次函数y=x2-(2m-1)x+m2-3m+4.
(1)探求m取不同值时,二次函数y的图象与x轴的交点个数.
(2)设二次函数y的图象与x轴的交点为A(x1,0),(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的函数表达式.
(1)探求m取不同值时,二次函数y的图象与x轴的交点个数.
(2)设二次函数y的图象与x轴的交点为A(x1,0),(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的函数表达式.
考点:抛物线与x轴的交点
专题:
分析:(1)解方程x2-(2m-1)x+m2-3m+4=0,根据b2-4ac>0,方程有2个根,b2-4ac=0,方程有一个根,b2-4ac<0,方程没有根即可解题;
(2)根据韦达定理可得x1+x2=-
,x1x2=
,根据x12+x22=5,即可求得m的值,即可求得点C和点M坐标,即可解题.
(2)根据韦达定理可得x1+x2=-
| b |
| a |
| c |
| a |
解答:解:(1)当y=0时,可得方程x2-(2m-1)x+m2-3m+4=0,
b2-4ac=(2m-1)2-4(m2-3m+4)=8m-15,
当8m-15>0时,即m>
时,方程有2个根,故二次函数y的图象与x轴的交点个数为2,
当8m-15=0时,即m=
时,方程有1个根,故二次函数y的图象与x轴的交点个数为1,
当8m-15<0时,即m<
时,方程有0个根,故二次函数y的图象与x轴的交点个数为0;
(2)∵x1+x2=-
=2m-1,x1x2=
=m2-3m+4,
∴x12+x22=(x1+x2)2-2x1x2=4m2-4m+1-2(m2-3m+4)=5,
化简得:m2+m-6=0,解得:m=-3或2,
∵m>
,
∴m=2,
∴抛物线解析式为y=x2-3x+2=(x-
)2-
,
∴顶点坐标为(
,-
),
∵x=0时,y=2,
∴点C坐标(0,2),
设直线CM解析式为y=kx+b,
代入C,M点得:y=-
x+2.
b2-4ac=(2m-1)2-4(m2-3m+4)=8m-15,
当8m-15>0时,即m>
| 15 |
| 8 |
当8m-15=0时,即m=
| 15 |
| 8 |
当8m-15<0时,即m<
| 15 |
| 8 |
(2)∵x1+x2=-
| b |
| a |
| c |
| a |
∴x12+x22=(x1+x2)2-2x1x2=4m2-4m+1-2(m2-3m+4)=5,
化简得:m2+m-6=0,解得:m=-3或2,
∵m>
| 15 |
| 8 |
∴m=2,
∴抛物线解析式为y=x2-3x+2=(x-
| 3 |
| 2 |
| 1 |
| 4 |
∴顶点坐标为(
| 3 |
| 2 |
| 1 |
| 4 |
∵x=0时,y=2,
∴点C坐标(0,2),
设直线CM解析式为y=kx+b,
代入C,M点得:y=-
| 3 |
| 2 |
点评:本题考查了一元二次方程的求解,考查了韦达定理的运用,考查了抛物线与y轴交点的求解,考查了抛物线顶点的求解,本题中求得m的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线开口向上,顶点坐标是(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
| A、x>3 | B、x<3 |
| C、x>1 | D、x<1 |
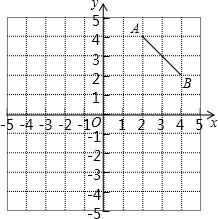 如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
如图在8×8的正方形网格中建立直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.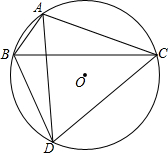 如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.
如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.