题目内容
16.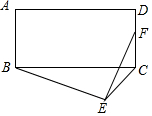 如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为( )
如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为( )| A. | $\frac{\sqrt{433}}{2}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{\sqrt{433}}{4}$ |
分析 由∠BEC=90°知点E在以BC为直径的⊙O上,连接FO并延长交⊙O于点E′,此时E′F最长,利用勾股定理求得OF=$\frac{13}{2}$,从而由E′F=OE′+OF可得答案.
解答 解:由题意知∠BEC=90°,
∴点E在以BC为直径的⊙O上,如图所示: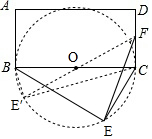
由图可知,连接FO并延长交⊙O于点E′,
此时E′F最长,
∵CO=$\frac{1}{2}$BC=6、FC=$\frac{1}{2}$CD=$\frac{5}{2}$,
∴OF=$\sqrt{O{C}^{2}+C{F}^{2}}$=$\sqrt{{6}^{2}+(\frac{5}{2})^{2}}$=$\frac{13}{2}$,
则E′F=OE′+OF=6+$\frac{13}{2}$=$\frac{25}{2}$,
故选:C.
点评 本题主要考查圆周角定理及勾股定理,根据圆周角定理得出点E在以BC为直径的⊙O上,从而确定出使EF最长的点E的位置是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
4. 如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
 如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )| A. | 140° | B. | 40° | C. | 100° | D. | 180° |
11.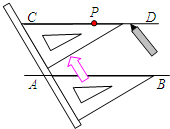 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )| A. | 同位角相等,两直线平行 | |
| B. | 内错角相等,两直线平行 | |
| C. | 同旁内角互补,两直线品行 | |
| D. | 过直线外一点有且只有一条直线与这条直线平行 |
1. 如图,与∠1是同位角的为( )
如图,与∠1是同位角的为( )
 如图,与∠1是同位角的为( )
如图,与∠1是同位角的为( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
8.与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{\frac{1}{8}}$ | C. | $\sqrt{0.2}$ | D. | $\sqrt{27}$ |
5.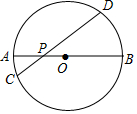 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )| A. | $\sqrt{15}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{15}$ | D. | 8 |