题目内容
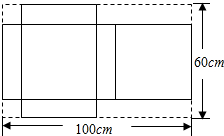 如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.
如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.考点:一元二次方程的应用
专题:几何图形问题
分析:此题可以设铁皮的各角应切去边长为xcm的正方形.则底面矩形的长是
(100-2x)cm,宽是(60-2x),然后根据等量关系:长方体盒子的底面积是1600cm2,列方程求解.
| 1 |
| 2 |
解答:解:设铁皮的各角应切去边长为xcm的正方形.则底面矩形的长是
(100-2x)cm,宽是(60-2x),依题意有
(100-2x)(60-2x)=1600,
则x2-80x+700=0,
(x-70)(x-10)=0,
解得x1=70(不合题意舍去),x2=10.
答:该盒子的高是10cm.
| 1 |
| 2 |
| 1 |
| 2 |
则x2-80x+700=0,
(x-70)(x-10)=0,
解得x1=70(不合题意舍去),x2=10.
答:该盒子的高是10cm.
点评:本题考查了一元二次方程的应用.在列方程的时候,弄清长方体盒子底面的长和宽,能够熟练运用因式分解法解方程.最后求得的解要注意检验看是否符合题意.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
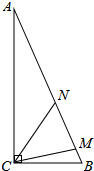 如图,在△ABC中,∠ACB=90°,AC=24,AB=25,AM=AC,BN=BC,则MN的长为( )
如图,在△ABC中,∠ACB=90°,AC=24,AB=25,AM=AC,BN=BC,则MN的长为( )| A、4 | B、5 | C、6 | D、7 |
已知⊙O的半径为5,点P在⊙O内,且PO=4,则过点P且弦长为整数的弦有( )条.
| A、5 | B、6 | C、7 | D、8 |
 已知,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,∠ADB=60°,E、F、G分别是OA、OB、CD的中点,判断△EFG的形状,并说明理由.
已知,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,∠ADB=60°,E、F、G分别是OA、OB、CD的中点,判断△EFG的形状,并说明理由.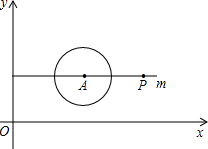 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(4,3),⊙A的半径为2,过点A作直线m∥x轴,点P在直线m上运动.当点P在⊙A上时,求点P的坐标.若点P的横坐标为12,试猜想直线OP与⊙A的位置关系,并证明你的猜想.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(4,3),⊙A的半径为2,过点A作直线m∥x轴,点P在直线m上运动.当点P在⊙A上时,求点P的坐标.若点P的横坐标为12,试猜想直线OP与⊙A的位置关系,并证明你的猜想. 如图,线段AB、CD相交于点O,E是△OCB内任一点,连接AE、DE,求∠A+∠B+∠C+∠D+∠AED的度数.
如图,线段AB、CD相交于点O,E是△OCB内任一点,连接AE、DE,求∠A+∠B+∠C+∠D+∠AED的度数. 如图,点A为正比例函数y=kx的图象上一点,过A作AB⊥x于B,交正比例函数y=x的图象于点C,且S△AOC=S△BOC,求k的值.
如图,点A为正比例函数y=kx的图象上一点,过A作AB⊥x于B,交正比例函数y=x的图象于点C,且S△AOC=S△BOC,求k的值.