题目内容
 如图,点A为正比例函数y=kx的图象上一点,过A作AB⊥x于B,交正比例函数y=x的图象于点C,且S△AOC=S△BOC,求k的值.
如图,点A为正比例函数y=kx的图象上一点,过A作AB⊥x于B,交正比例函数y=x的图象于点C,且S△AOC=S△BOC,求k的值.考点:两条直线相交或平行问题
专题:
分析:首先设A点坐标为(x1,y1),利用三角形的面积公式表示出S△AOC=
AC•OB,S△BOC=
BC•OB,进而得到BC=AC,再根据正比例函数y=x可得∠BOC=45°,所以BC=BO=x1,则AB=2BC=2x1,进而得到A的坐标为(x1,2x1),再代入y=kx可得k的值.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:设A点坐标为(x1,y1),
解:设A点坐标为(x1,y1),
∵△AOB是直角三角形,
∴S△AOC=
AC•OB,S△BOC=
BC•OB,
∴BC=AC,
∵C是y=x上的一点,
∴∠BOC=45度
所以BC=BO=x1,
于是AB=2BC=2x1,
所以A的坐标为(x1,2x1),
所以代入正比例函数关系式y=kx可得:k=2.
 解:设A点坐标为(x1,y1),
解:设A点坐标为(x1,y1),∵△AOB是直角三角形,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BC=AC,
∵C是y=x上的一点,
∴∠BOC=45度
所以BC=BO=x1,
于是AB=2BC=2x1,
所以A的坐标为(x1,2x1),
所以代入正比例函数关系式y=kx可得:k=2.
点评:此题主要考查了三角形的面积计算,以及待定系数法求一次函数解析式,关键是正确分析出AB=2BC.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
下列说法正确的是( )
| A、弦是直径 |
| B、半圆是弧 |
| C、长度相等的弧是等弧 |
| D、过圆心的线段是直径 |
在锐角三角形中,最大角x的取值范围是( )
| A、0°<x<90° |
| B、60°<x<90° |
| C、60°<x<180° |
| D、60°≤x<90° |
在△ABC与△DEF中,AB=DF,AC=DE,CB=EF,那么( )
| A、△ABC≌△DEF |
| B、△ABC≌△DFE |
| C、△ABC≌△EDF |
| D、△ABC≌△EFD |
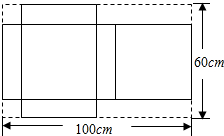 如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.
如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.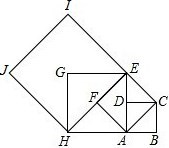 如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….
如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….