题目内容
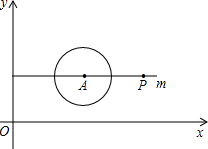 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(4,3),⊙A的半径为2,过点A作直线m∥x轴,点P在直线m上运动.当点P在⊙A上时,求点P的坐标.若点P的横坐标为12,试猜想直线OP与⊙A的位置关系,并证明你的猜想.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(4,3),⊙A的半径为2,过点A作直线m∥x轴,点P在直线m上运动.当点P在⊙A上时,求点P的坐标.若点P的横坐标为12,试猜想直线OP与⊙A的位置关系,并证明你的猜想.考点:直线与圆的位置关系,坐标与图形性质
专题:
分析:过A作AD⊥OP,再由OB⊥BP,得到一对直角相等,再由一对公共角,利用两对对应角相等的两三角形相似可得出△APD与△OPB相似,根据相似得比例,将各自的值代入求出AD的长,与半径r=2比较大小,即可判断出直线OP与圆A的位置关系.
解答: 解:直线OP与⊙A相交.
解:直线OP与⊙A相交.
理由:过点A作AD⊥OP于D,如图所示:
可得∠ADP=90°,
又∵∠PBO=90°,
∴∠ADP=∠PBO,
又∵∠APD=∠OPB,
∴△PAD∽△POB,
又∵PA=PB-AB=12-4=8,OB=3,
在直角△OBP中,OB=3,BP=12,
根据勾股定理得:OP=
=
,
∴
=
,即
=
,
解得:AD=
≈1.9<2=r,
∴直线OP与⊙A相交.
 解:直线OP与⊙A相交.
解:直线OP与⊙A相交.理由:过点A作AD⊥OP于D,如图所示:
可得∠ADP=90°,
又∵∠PBO=90°,
∴∠ADP=∠PBO,
又∵∠APD=∠OPB,
∴△PAD∽△POB,
又∵PA=PB-AB=12-4=8,OB=3,
在直角△OBP中,OB=3,BP=12,
根据勾股定理得:OP=
| BO2+BP2 |
| 153 |
∴
| PA |
| OP |
| AD |
| OB |
| 8 | ||
|
| AD |
| 3 |
解得:AD=
24
| ||
| 153 |
∴直线OP与⊙A相交.
点评:此题考查了直线与圆的位置关系,涉及的知识有:勾股定理,相似三角形的判定与性质,以及坐标与图形性质,直线与圆的位置关系可以由d与r的大小来判断(r表示圆的半径,d表示圆心到直线的距离),当d<r时,直线与圆相交;当d=r时,直线与圆相切;当d>r时,直线与圆相离.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
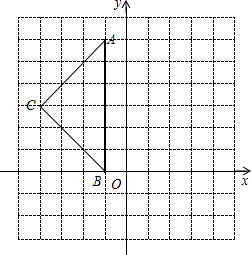 如图,在平面直角坐标系中,A(-1,6)、B(-1,0)、C(-4,3).
如图,在平面直角坐标系中,A(-1,6)、B(-1,0)、C(-4,3).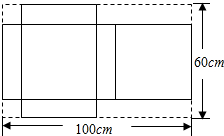 如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.
如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.