题目内容
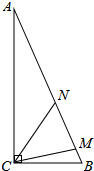 如图,在△ABC中,∠ACB=90°,AC=24,AB=25,AM=AC,BN=BC,则MN的长为( )
如图,在△ABC中,∠ACB=90°,AC=24,AB=25,AM=AC,BN=BC,则MN的长为( )| A、4 | B、5 | C、6 | D、7 |
考点:勾股定理
专题:
分析:先根据勾股定理求出BC的长,再根据MN=AM+BN-AB即可得出结论.
解答:解:∵在Rt△ABC中,∠ACB=90°,AC=24,AB=25,
∴BC=
=
=7.
又∵AC=24,BC=7,AM=AC,BN=BC,
∴AM=24,BN=7,
∴MN=AM+BN-AB=24+7-25=6.
故选C.
∴BC=
| AB2-AC2 |
| 252-242 |
又∵AC=24,BC=7,AM=AC,BN=BC,
∴AM=24,BN=7,
∴MN=AM+BN-AB=24+7-25=6.
故选C.
点评:本题综合考查的是勾股定理,根据题意找到关系MN=AM+BN-AB是解答此题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、弦是直径 |
| B、半圆是弧 |
| C、长度相等的弧是等弧 |
| D、过圆心的线段是直径 |
 如图,C在直线BE上,∠ABC与∠ACE的角平分线交于点A1.
如图,C在直线BE上,∠ABC与∠ACE的角平分线交于点A1.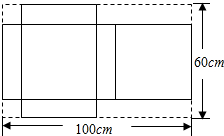 如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.
如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.