题目内容
 如图,线段AB、CD相交于点O,E是△OCB内任一点,连接AE、DE,求∠A+∠B+∠C+∠D+∠AED的度数.
如图,线段AB、CD相交于点O,E是△OCB内任一点,连接AE、DE,求∠A+∠B+∠C+∠D+∠AED的度数.考点:三角形内角和定理
专题:
分析:连接AD,求出∠C+∠B=∠OAD+∠ODA,根据三角形内角和定理求出即可.
解答:解:
连接AD,
∠AOD=∠BOC,∠C+∠B+∠COB=180°,∠AOD+∠OAD+∠ODA=180°,
∴∠C+∠B=∠OAD+∠ODA,
在△ADE中,∠AED+∠EAB+∠OAD+∠ODA+∠EDC=180°,
即∠A+∠B+∠C+∠D+∠AED=180°.

连接AD,
∠AOD=∠BOC,∠C+∠B+∠COB=180°,∠AOD+∠OAD+∠ODA=180°,
∴∠C+∠B=∠OAD+∠ODA,
在△ADE中,∠AED+∠EAB+∠OAD+∠ODA+∠EDC=180°,
即∠A+∠B+∠C+∠D+∠AED=180°.
点评:本题考查了三角形内角和定理的应用,注意:三角形的内角和等于180°,题目比较典型,难度适中.

练习册系列答案
相关题目
下列说法正确的是( )
| A、弦是直径 |
| B、半圆是弧 |
| C、长度相等的弧是等弧 |
| D、过圆心的线段是直径 |
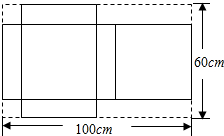 如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.
如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高. 如图某菜农在生态园蔬菜基地搭建了一个横截面位圆弧的蔬菜大棚大棚的跨度(弦AB的长)为根号
如图某菜农在生态园蔬菜基地搭建了一个横截面位圆弧的蔬菜大棚大棚的跨度(弦AB的长)为根号