题目内容
 等边三角形ABC中,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.∠BPF=60°,求证:△APE∽△BAE.
等边三角形ABC中,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.∠BPF=60°,求证:△APE∽△BAE.考点:相似三角形的判定
专题:证明题
分析:先根据等边三角形的性质得∠BAC=60°,即∠BAP+∠PAE=60°,再根据三角形外角性质有∠BPF=∠ABP+∠BAP=60°,则∠ABP=∠PAE,加上∠AEP=∠BEA,于是根据相似三角形的判定即可得到△APE∽△BAE.
解答:证明:∵△ABC为等边三角形,
∴∠BAC=60°,即∠BAP+∠PAE=60°,
∵∠BPF=60°,
而∠BPF=∠ABP+∠BAP,
∴∠ABP+∠BAP=60°,
∴∠ABP=∠PAE,
∵∠AEP=∠BEA,
∴△APE∽△BAE.
∴∠BAC=60°,即∠BAP+∠PAE=60°,
∵∠BPF=60°,
而∠BPF=∠ABP+∠BAP,
∴∠ABP+∠BAP=60°,
∴∠ABP=∠PAE,
∵∠AEP=∠BEA,
∴△APE∽△BAE.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等边三角形的性质.

练习册系列答案
相关题目
一元二次方程x2-x+a=0的一根为-1,则a的值为( )
| A、0 | B、1 | C、2 | D、-2 |
 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BD:DC=3:2,点D到AB的距离为6,则BC的长是
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BD:DC=3:2,点D到AB的距离为6,则BC的长是 如图,直线l过点A(4,0)、B(0,4)两点,它与抛物线y-ax2在第一象限内相交于点P,又知△AOP的面积为
如图,直线l过点A(4,0)、B(0,4)两点,它与抛物线y-ax2在第一象限内相交于点P,又知△AOP的面积为 已知,如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知,如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
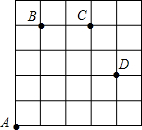 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中 如图,⊙O的半径OB=5cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8cm,求AB的长.
如图,⊙O的半径OB=5cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8cm,求AB的长.