如图的4×4的正方形网格中.有A.B两点.在直线a上求一点P.使PA+PB最短.则点P应选在( )A．C点B．D点C．E点D．F点题目和参考答案——青夏教育精英家教网—

题目内容

6．

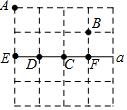如图的4×4的正方形网格中，有A、B两点，在直线a上求一点P，使PA+PB最短，则点P应选在（　　）

A．

C点

B．

D点

C．

E点

D．

F点

分析首先求得点A关于直线a的对称点A′，连接A′B，即可求得答案．

解答解：如图，点A′是点A关于直线a的对称点，连接A′B，则A′B与直线a的交点，即为点P，此时PA+PB最短，
∵A′B与直线a交于点C，
∴点P应选C点．
故选A．

点评此题考查了最短路径问题．注意首先作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点．

练习册系列答案

17．

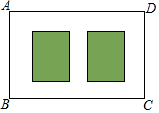要对一块长90米，宽40米的矩形荒地ABCD进行绿化和硬化，设计方案如图所示，矩形P，Q为两块绿地，其余为硬化路面，P、Q两块绿地周围的硬化路面宽度都相等，并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{3}$，求P、Q两块绿地周围的硬化路面的宽．

1．化简
（1）$\sqrt{8}$+$\sqrt{18}$；
（2）（$\sqrt{6}$-2$\sqrt{3}$）×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$．

11．（1）求x的值：（2x）²=0.25；
（2）计算：$\sqrt{（-6）^{2}}$-$\root{3}{-8}$+（-$\sqrt{5}$）²．

18．一条关于数学学习方法的微博在一周内转发了318000次，将318000用科学记数法可以表示为（　　）

15．

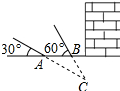如图，某武警部队在一次地震抢险救灾行动中，探险队员在相距4米的水平地面A，B两处均探测出建筑物下方C处有生命迹象，已知在A处测得探测线与地面的夹角为30°，在B处测得探测线与地面的夹角为60°，求该生命迹象C处与地面的距离．（结果精确到0.1米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

17．（1）计算：$\sqrt{8}$-（-2016）⁰+|-3|-4cos45°
（2）化简求值：（$\frac{a}{a+2}$+$\frac{1}{{a}^{2}-4}$）÷$\frac{a-1}{a+2}$+$\frac{1}{a-2}$，其中a=2+$\sqrt{2}$．

试题分类