题目内容
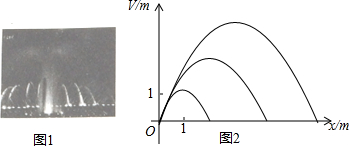
1.音乐喷泉可以使喷水造型随音乐的节奏起伏变化而变化,市民广场的音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18米,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.(1)若已知k=1,且喷出的抛物线水线最大高度达3米,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,求此时喷出的抛物线水线最大高度.
(3)若a=-$\frac{2}{7}$,要使喷出的抛物线水落地时离岸边不能少于$\frac{1}{2}$米且不能超出2米,求k的范围.
分析 (1)由题意抛物线的顶点坐标为(3,3),根据顶点坐标公式可得$\left\{\begin{array}{l}{-\frac{b}{2a}=3}\\{\frac{-{b}^{2}}{4a}=3}\end{array}\right.$,由此即可解决问题.
(2)判断出顶点坐标,即可解决问题.
(3)根据抛物线的对称轴的位置,列出不等式,求出b的取值范围$\frac{36}{7}$≤b≤$\frac{39}{7}$,当b=$\frac{39}{7}$时,抛物线的顶点坐标($\frac{39}{4}$,$\frac{1521}{56}$),此时$\frac{1521}{56}$=$\frac{39}{4}$k,解得k=$\frac{39}{14}$,
当b=$\frac{36}{7}$时,抛物线的顶点坐标为(9,$\frac{162}{7}$),此时$\frac{162}{7}$=9k,解得k=$\frac{18}{7}$,由此可得k的取值范围为$\frac{18}{7}$≤k$≤\frac{39}{14}$.
解答 解:(1)由题意抛物线的顶点坐标为(3,3),
∴$\left\{\begin{array}{l}{-\frac{b}{2a}=3}\\{\frac{-{b}^{2}}{4a}=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=2}\end{array}\right.$,
∴a=-$\frac{1}{3}$,b=2.
(2)由题意抛物线的对称轴x=9,
∵顶点在直线y=x上,
∴顶点坐标为(9,9),
∴此时喷出的抛物线水线最大高度为9米.
(3)由题意9≤-$\frac{b}{2a}$≤$\frac{39}{4}$,
∴9≤$\frac{7}{4}$≤$\frac{39}{4}$,
∴$\frac{36}{7}$≤b≤$\frac{39}{7}$,
当b=$\frac{39}{7}$时,抛物线的顶点坐标($\frac{39}{4}$,$\frac{1521}{56}$),此时$\frac{1521}{56}$=$\frac{39}{4}$k,解得k=$\frac{39}{14}$,
当b=$\frac{36}{7}$时,抛物线的顶点坐标为(9,$\frac{162}{7}$),此时$\frac{162}{7}$=9k,解得k=$\frac{18}{7}$,
∴k的取值范围为$\frac{18}{7}$≤k$≤\frac{39}{14}$.
点评 本题考查二次函数的应用、一次函数的应用等知识,解题的关键是灵活运用为二次函数的性质解决问题,属于中考常考题型.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案| A. | -2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | 5 |
| 运输工具 | 平均速度(千米/小时) | 运费(元/千米) | 装卸总费用(元) |
| 火车 | 120 | 20 | 2400 |
| 汽车 | 100 | 25 | 1600 |
(2)如果汽车运输总费用比火车运输总费用多1600,求A县与B市之间的路程为多少?
(3)如果小李想将这批水果运往C市销售,选择哪种运输工具比较合算?请说明你的理由.

 如图是某地的长方形大理石广场示意图,如果小王从A角走到C角,至少走50米.
如图是某地的长方形大理石广场示意图,如果小王从A角走到C角,至少走50米.