题目内容
11.如图,在直线l上依次摆放着4031个正方形,已知斜放着的2015个正方形的面积分别是1、2、3、…、2015,正放置的2016个正方形的面积依次是S1、S2、S3…、S2016,那么S1+S2+S3+…+S2016=1016064.
分析 运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
解答 解:解:观察发现,
∵AB=BE,∠ACB=∠BDE=90°,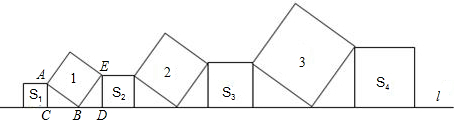
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD,
在△ABC和△BED中,
$\left\{\begin{array}{l}{∠ACB=∠BDE=90°}\\{∠BAC=∠EBD}\\{AB=BE}\end{array}\right.$,
∴△ABC≌△BDE(AAS),
∴BC=ED,
∵AB2=AC2+BC2,
∴AB2=AC2+ED2=S1+S2,
即S1+S2=1,
同理S3+S4=3,S5+S6=5,…,S2011+S2012=2011,
则S1+S2+S3+S4+…S2016=1+3+5+…+2015=$\frac{1+2015}{2}$×$\frac{1+2015}{2}$=1016064,
故答案为1016064
点评 此题考查了勾股定理,全等三角形的判定与性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
19.能说明命题“对于任何实数a,a2≥a”是假命题的一个反例可以是( )
| A. | a=-2 | B. | a=1 | C. | a=0 | D. | a=0.2 |
6.下列四组线段中,能组成三角形的是( )
| A. | 2cm,3cm,4cm | B. | 3cm,4cm,7cm | C. | 4cm,6cm,2cm | D. | 7cm,10cm,2cm |
16.4的算术平方根是( )
| A. | y=2x-1 | B. | 2 | C. | 4 | D. | ±2 |
20.下列同一个几何体中,主视图与俯视图不同的是( )
| A. |  圆柱 | B. |  正方体 | C. |  圆锥 | D. |  球 |
 已知:如图,△ABC是等腰三角形,AB=AC,现要在AB边上确定一点D,使点D到点A的距离与点D到点C的距离相等.
已知:如图,△ABC是等腰三角形,AB=AC,现要在AB边上确定一点D,使点D到点A的距离与点D到点C的距离相等.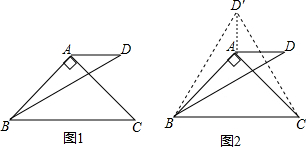
 如图,在平面直角坐标系中,一次函数y=kx+4的图象经过点A(1,3),点B是一次函数y=kx+4的图象与正比例函数y=$\frac{1}{3}$x的图象的交点.
如图,在平面直角坐标系中,一次函数y=kx+4的图象经过点A(1,3),点B是一次函数y=kx+4的图象与正比例函数y=$\frac{1}{3}$x的图象的交点.