Question

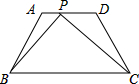如图，在梯形ABCD中，AD∥BC，AB=CD=2，AD=5，在AD边上是否存在一点P，使得△ABP与△DPC相似？若存在，求出线段AP的长；若不存在，请说明理由．

Answer 1

考点：相似三角形的判定

专题：存在型

分析：由AD∥BC，AB=CD=2得到梯形ABCD为等腰梯形，所以∠A=∠D，根据两组对应边的比相等且夹角对应相等的两个三角形相似得到当

AB

CD

=

AP

DP

时，△ABP∽△DCP或当

AB

DP

=

AP

DC

时，△ABP∽△DPC，然后利用比例式分别求出AP的长．

解答：解：存在．理由如下：
∵AD∥BC，AB=CD=2，
∴梯形ABCD为等腰梯形，
∴∠A=∠D，
∴当

AB

CD

=

AP

DP

时，△ABP∽△DCP，即

2

2

=

AP

DP

，所以AP=DP，而AD=5，所以AP=

1

2

AD=

5

2

；
当

AB

DP

=

AP

DC

时，△ABP∽△DPC，即

2

DP

=

AP

2

，所以AP（5-AP）=4，解得AP=1或AP=4（舍去），
∴当AP=1或

5

2

时，△ABP与△DPC相似．

点评：本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．也考查了等腰梯形的性质和分类讨论的思想的应用．