题目内容
13.已知关于x的一元二次方程x2-(m+6)x+3m+9=0的两个实数根分别为x1,x2.(1)求证:该一元二次方程总有两个实数根;
(2)若n=$\frac{8}{{x}_{1}+{x}_{2}-6}$,判断动点P(m,n)所形成的函数图象是否经过点A(4,2),并说明理由.
分析 (1)先计算判别式的值得到△=m2,易得△≥0,则根据判别式的意义可判断该一元二次方程总有两个实数根;
(2)由根与系数的关系得到x1+x2=m+6,则n=$\frac{6}{m}$,然后可根据反比例函数图象上点的坐标特征可判断动点P(m,n)所形成的函数图象经过点A(4,2).
解答 (1)证明:△=(m+6)2-4(3m+9)
=m2,
∵m2≥0,即△≥0,
∴该一元二次方程总有两个实数根;
(2)解:动点P(m,n)所形成的函数图象经过点A(4,2).理由如下:
根据题意得x1+x2=m+6,
而n=$\frac{8}{{x}_{1}+{x}_{2}-6}$,
∴n=$\frac{8}{m+6-6}$,
即n=$\frac{8}{m}$,
当m=4时,n=$\frac{8}{4}$=2,
∴动点P(m,n)所形成的函数图象经过点A(4,2).
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.将抛物线y=3x2向右平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( )
| A. | y=3(x+2)2+3 | B. | y=3(x+2)2-3 | C. | y=3(x-2)2+3 | D. | y=3(x-2)2-3 |
1.下列各点中位于第三象限的点是( )
| A. | (-2,-1) | B. | (1,-2) | C. | (2,1) | D. | (2,-1) |
8.若不等式2x<4+a与不等式3x-2<2x+3的解集相同,则a的值是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
 如图是正方体的展开图,则原正方体相对两个面上的数字和的最小值是6..
如图是正方体的展开图,则原正方体相对两个面上的数字和的最小值是6..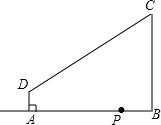 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )