题目内容
3．将抛物线y=3x2向右平移2个单位，再向上平移3个单位，得到的抛物线的解析式是（ ）| A． | y=3（x+2）2+3 | B． | y=3（x+2）2-3 | C． | y=3（x-2）2+3 | D． | y=3（x-2）2-3 |
分析 先由而次函数的性质得到抛物线y=3x2的顶点坐标为（0，0），再根据点平移的规律，点（0，0）平移后所得对应点的坐标为（2，3），然后根据顶点式写出平移后的抛物线的解析式．
解答 解：抛物线y=3x2的顶点坐标为（0，0），把（0，0）向右平移2个单位，再向上平移3个单位所得对应点的坐标为（2，3），所以平移后的抛物线的解析式是y=3（x-2）2+3．
故选C．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．解决此题的关键是把抛物线平移的问题转化为顶点平移的问题．
练习册系列答案
相关题目
14．函数y=（m-2）x2+5x是为关于x的二次函数，其图象开口向下，则m的取值范围是（ ）
| A． | m＜2 | B． | m＞2 | C． | m≥2 | D． | m≤2 |
8．下列计算正确的是（ ）
| A． | $\sqrt{16}=±4$ | B． | $\sqrt{8}-2\sqrt{2}=0$ | C． | $\sqrt{24}-\sqrt{4}$ | D． | $（{2-\sqrt{5}}）（{2+\sqrt{5}}）=1$ |
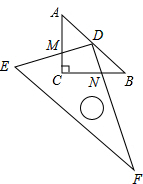如图，在△ABC中，AC=BC=1，∠ACB=90°，把一块含30°角的直角三角尺（△DEF）的直角顶点D放在AB边的中点上，将直角三角尺绕点D转动，其中DE交AC于点M，DF交BC于点N．
12．若点P（-a，a-3）关于原点对称的点是第二象限内的点，则a满足（ ）
| A． | a＞3 | B． | 0＜a≤3 | C． | a＜0 | D． | a＜0或a＞3 |