题目内容
2.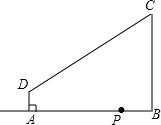 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 设AP=x,则BP=7-x,分两种情况:①当$\frac{AP}{AD}=\frac{BP}{BC}$时;②当$\frac{AP}{AD}=\frac{BC}{BP}$时;③当P点在A点左侧时还有二种情况,分别得出x的方程,解方程得出AP的长,即可得出结果.
解答 解:AD∥BC,∠ABC=90°,
∴∠PAD+∠ABC=180°,
∴∠PAD=90°,
设AP=x,则BP=7-x,
分两种情况:
①当$\frac{AP}{AD}=\frac{BP}{BC}$时,即$\frac{x}{2}=\frac{7-x}{6}$,
解得:x=$\frac{7}{4}$;
②当$\frac{AP}{AD}=\frac{BC}{BP}$时,即$\frac{x}{2}=\frac{6}{7-x}$,
解得:x=3,或x=4;
③当P点在A点左侧时还有二种情况,x=$\frac{7}{2}$或x=$\frac{-7+\sqrt{97}}{2}$,
综上所述:当AP=$\frac{7}{4}$或3或4或$\frac{7}{2}$或$\frac{-7+\sqrt{97}}{2}$时,△PAD与△PBC是相似三角形;
即满足条件的点P个数是5个.
故选:A.
点评 本题考查了相似三角形的判定、平行线的性质、解方程;熟练掌握相似三角形的判定定理,通过分类讨论得出比例式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若点P(-a,a-3)关于原点对称的点是第二象限内的点,则a满足( )
| A. | a>3 | B. | 0<a≤3 | C. | a<0 | D. | a<0或a>3 |
17.已知a=2cm,b=10mm,那么$\frac{a}{b}$的值为( )
| A. | $\frac{1}{50}$ | B. | $\frac{1}{5}$ | C. | 2 | D. | $\frac{5}{2}$ |
14.若M是线段AB的黄金分割点(MA>MB),设AB=2cm,则线段MA的长为( )cm.
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | 3-$\sqrt{5}$ | C. | 1 | D. | $\sqrt{5}$-1 |
12. 如图,在△ABC中,AC=BC,BD⊥AC于点D,以点C为旋转中心,将△BCD顺时针旋转,得到△ACD′.若∠ABD=35°,则∠BCD′的大小为( )
如图,在△ABC中,AC=BC,BD⊥AC于点D,以点C为旋转中心,将△BCD顺时针旋转,得到△ACD′.若∠ABD=35°,则∠BCD′的大小为( )
 如图,在△ABC中,AC=BC,BD⊥AC于点D,以点C为旋转中心,将△BCD顺时针旋转,得到△ACD′.若∠ABD=35°,则∠BCD′的大小为( )
如图,在△ABC中,AC=BC,BD⊥AC于点D,以点C为旋转中心,将△BCD顺时针旋转,得到△ACD′.若∠ABD=35°,则∠BCD′的大小为( )| A. | 140° | B. | 145° | C. | 150° | D. | 155° |
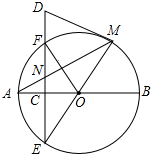 如图,AB为⊙O的直径,C为OA的中点,过点C作EF⊥AB,交⊙O于点E,F,连接EO并延长交⊙O于点M,过点M作⊙O的切线DM,与EF的延长线交于点D,切点为M,连接AM,交EF于点N,连接OF.
如图,AB为⊙O的直径,C为OA的中点,过点C作EF⊥AB,交⊙O于点E,F,连接EO并延长交⊙O于点M,过点M作⊙O的切线DM,与EF的延长线交于点D,切点为M,连接AM,交EF于点N,连接OF.