题目内容
20.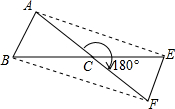 已知:如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
已知:如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.(1)△ABC与△FEC具有怎样的对称关系?
(2)若△ABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ABC为多少度时,四边形ABFE为矩形?说明理由.
分析 (1)根据中心对称的定义进行判断;
(2)先利用中心对称的性质得到CA=CF,CB=CE,则可判断四边形ABFE为平行四边形,根据平行四边形的性质得S四边形ABFE=4S△ABC=12cm2;
(3)由于AB=AC,当∠ABC=60°时,可判断△ABC为等边三角形,则AC=BC,易得CA=CF=CB=CE,于是可根据矩形的判定方法判定四边形ABFE为矩形.
解答 解:(1)∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC与△FEC关于点C中心对称;
(2)∵△ABC与△FEC关于点C中心对称,
∴CA=CF,CB=CE,
∴四边形ABFE为平行四边形,
∴S四边形ABFE=4S△ABC=4×3=12(cm2);
(3)当∠ABC为60度时,四边形ABFE为矩形.理由如下:
∵AB=AC,∠ABC=60°,
∴△ABC为等边三角形,
∴AC=BC,
而CA=CF,CB=CE,
∴CA=CF=CB=CE,
∴四边形ABFE为矩形.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了矩形的判定方法.

练习册系列答案
相关题目
5.下面计算正确的是( )
| A. | 5x2-x2=5 | B. | 4a2+3a2=7a4 | C. | 5+y=5y | D. | -0.25mn+$\frac{1}{4}$mn=0 |
12.等腰三角形的周长为10,底边长y与腰x的函数关系式是y=10-2x,则自变量x的取值范围是( )
| A. | x>0 | B. | x<5 | C. | 0<x<5 | D. | 2.5<x<5 |
9.如果关于x的方程(m+1)x2+(m-1)x+m=0是一元一次方程,则m的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 1或-1 |
 如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,并且BE=CF,求证:点D在BC的垂直平分线上.
如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,并且BE=CF,求证:点D在BC的垂直平分线上.