题目内容
10.已知x=$\sqrt{5}+2$,y=$\sqrt{5}-2$,求下列各式的值:(1)x2-2xy+y2
(2)x2-y2.
分析 (1)利用完全平方公式因式分解,再进一步代入求得数值;
(2)利用平方差公式因式分解,再进一步代入求得数值.
解答 解:(1)原式=(x-y)2=($\sqrt{5}+2$-$\sqrt{5}$+2)2=16;
(2)原式=(x+y)(x-y)=($\sqrt{5}+2$+$\sqrt{5}$-2)($\sqrt{5}+2$-$\sqrt{5}$+2)=8$\sqrt{5}$.
点评 此题考查二次根式的化简求值,因式分解的运用,掌握完全平方公式和平方差公式是解决问题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
5.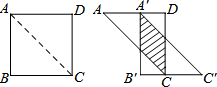 如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )
如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )
 如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )
如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )| A. | 6cm | B. | 8cm | C. | 6cm或8cm | D. | 4cm或8cm |
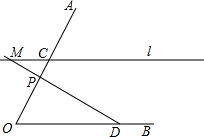 如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.
如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.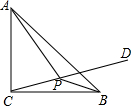 如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )
如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )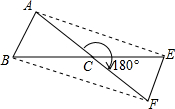 已知:如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
已知:如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.