题目内容
3.解方程:(1)5(2x-3)-6(1+2x)=3
(2)$\frac{x-1}{2}-\frac{2x+3}{3}=1$
(3)3-$\frac{x-1}{2}$=3x-1
(4)$\frac{5x+1}{3}$-$\frac{2x-1}{6}$=1.
(5)2[2(3x+1)-4]=2x-5
(6)$\frac{3-7x}{5}=\frac{1-4x}{3}-1$.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(5)方程去括号,移项合并,把x系数化为1,即可求出解;
(6)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号得:10x-15-6-12x=3,
移项合并得:-2x=24,
解得:x=-12;
(2)去分母得:3x-3-4x-6=6,
移项合并得:-x=15,
解得:x=-15;
(3)去分母得:6-x+1=6x-2,
移项合并得:7x=9,
解得:x=$\frac{9}{7}$;
(4)去分母得:10x+2-2x+1=6,
移项合并得:8x=3,
解得:x=$\frac{3}{8}$;
(5)去括号得:12x+4-8=2x-5,
移项合并得:10x=-1,
解得:x=-$\frac{1}{10}$;
(6)去分母得:9-21x=5-20x-15,
移项合并得:x=19.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
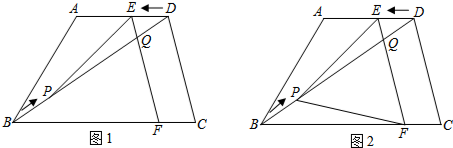
14. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②$\frac{FP}{PH}$=$\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.
其中正确的是( )
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②$\frac{FP}{PH}$=$\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.
其中正确的是( )
| A. | ①②③④ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
8.有一枚质地均匀的正方体骰子,六个面分别写有1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面朝上的那一个数字”.先后抛掷这枚骰子两次,得到的数字分别记为b和c,则当x>-3时,函数y=x2+bx+c随x的增大而增大的概率是( )
| A. | $\frac{11}{36}$ | B. | $\frac{5}{36}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
12. 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )
 如图所示的几何体的俯视图为( )
如图所示的几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
 苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1)
苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1) 如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.