题目内容
 如图,一次函数y1=ax+b和y2=bx+a(a≠0,b≠0)在同一坐标系的图象.则
如图,一次函数y1=ax+b和y2=bx+a(a≠0,b≠0)在同一坐标系的图象.则
|
|
| A、m>0,n>0 |
| B、m>0,n<0 |
| C、m<0,n>0 |
| D、m<0,n<0 |
考点:一次函数与二元一次方程(组)
专题:
分析:方程组的解实际上是两个一次函数图象的交点的横纵坐标,而交点在一象限,从而得到m,n的范围.
解答:
解:∵方程组
的解即是一次函数y1=ax+b和y2=bx+a的交点坐标,
由图象可知,交点(m,n)在第一象限,
∴m>0,n>0.
故选A.
|
由图象可知,交点(m,n)在第一象限,
∴m>0,n>0.
故选A.
点评:本题考查了二元一次方程组与一次函数的关系,理解点在图象上点的横纵坐标满足它的解析式,求图象交点的坐标常转化为求方程组的解.

练习册系列答案
相关题目
比较大小:-22,(-
)2,(-
)3,正确的是( )
| 1 |
| 2 |
| 1 |
| 3 |
A、-22>(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
在实数-3、0、2、3中,最小的实数是( )
| A、-3 | B、0 | C、2 | D、3 |
已知正比例函数y=(m+1)x,y随x的增大而减小,则m的取值范围是( )
| A、m<-1 | B、m>-1 |
| C、m≥-1 | D、m≤-1 |
 的图象经过点B(
的图象经过点B( ,0),且与反比例函数
,0),且与反比例函数 (
( 为不等于0的常数)的图象在第一象限交于点
为不等于0的常数)的图象在第一象限交于点 (1,
(1, ).求:
).求:
 时,反比例函数
时,反比例函数 的取值范围.
的取值范围.  ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )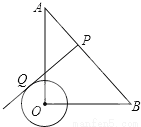
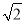 C.
C.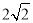 D.
D. 将长方形OABC先向上平移1个单位长度,再向左平移2个单位长度得新长方形D′A′B′C′,设A′B′与BC交于点M,求四边形A′MCO的面积.
将长方形OABC先向上平移1个单位长度,再向左平移2个单位长度得新长方形D′A′B′C′,设A′B′与BC交于点M,求四边形A′MCO的面积.