题目内容
已知:x,y为实数,且y<
+
+
,求x-1+
的值.
| x-1 |
| 1-x |
| 1 |
| 2 |
| y-1 | ||
|
考点:二次根式的化简求值,二次根式有意义的条件
专题:计算题
分析:先根据二次根式有意义的条件得到x=1,则y<
,再根据二次根式的性质对原式进行化简得到原式=
-1,然后把x=1代入计算即可.
| 1 |
| 2 |
| 1 |
| x |
解答:
解:根据题意得x-1≥0且1-x≥0,解得x=1,
则y<
,
原式=
+
=
+
=
+
=1-1
=0.
则y<
| 1 |
| 2 |
原式=
| 1 |
| x |
| y-1 | ||
|
=
| 1 |
| x |
| y-1 |
| |y-1| |
=
| 1 |
| x |
| y-1 |
| -(y-1) |
=1-1
=0.
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值;二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
 如图,一次函数y1=ax+b和y2=bx+a(a≠0,b≠0)在同一坐标系的图象.则
如图,一次函数y1=ax+b和y2=bx+a(a≠0,b≠0)在同一坐标系的图象.则
|
|
| A、m>0,n>0 |
| B、m>0,n<0 |
| C、m<0,n>0 |
| D、m<0,n<0 |
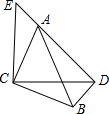 如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若
如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若 如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,BD的垂直平分线MN交AB于的E,连接DE,求证:AB=AC+CD.
如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,BD的垂直平分线MN交AB于的E,连接DE,求证:AB=AC+CD.