题目内容
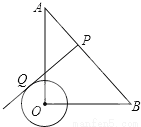
如图,在Rt△AOB中,OA=OB=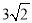 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.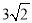 -1 B.2+
-1 B.2+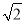 C.
C.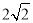 D.
D.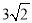
C.
【解析】
试题分析:连接OP、OQ.

∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3 ,
,
∴AB= OA=6,
OA=6,
∴OP= ,
,
∴PQ= .
.
故选C.
考点:切线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一次函数y1=ax+b和y2=bx+a(a≠0,b≠0)在同一坐标系的图象.则
如图,一次函数y1=ax+b和y2=bx+a(a≠0,b≠0)在同一坐标系的图象.则
|
|
| A、m>0,n>0 |
| B、m>0,n<0 |
| C、m<0,n>0 |
| D、m<0,n<0 |
 与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO= .
.
 的结果是( )
的结果是( ) C.
C.  D. ﹣2
D. ﹣2
 x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 .
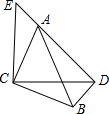 如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若
如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若