题目内容
王大爷有农田20块和现金4000元,计划今年种植水稻和小麦.这两种农作物每块天地的成本、产量及每公斤的收益如下表:
若王大爷用x块地种植水稻,一个收获季的收益共为y元.
(1)请写出y与x之间的函数关系.
(2)王大爷应如何分配种植面积(取整数),才能获得最大利益?
| 水稻 | 小麦 | |
| 每块地成本 | 240元 | 80元 |
| 每块地产量 | 800公斤 | 200公斤 |
| 每块地收益 | 3元/公斤 | 5元/公斤 |
(1)请写出y与x之间的函数关系.
(2)王大爷应如何分配种植面积(取整数),才能获得最大利益?
考点:一次函数的应用
专题:
分析:(1)根据题意表示出成本与收益进而得出函数解析式;
(2)根据题意得出x的最值,进而利用一次函数增减性得出答案.
(2)根据题意得出x的最值,进而利用一次函数增减性得出答案.
解答:解:(1)由题意可得:
y=3×800x-240x+5×200(20-x)-80x
=1080x+20000;
(2)∵王大爷有农田20块和现金4000元,由图表可得:
∴240x+80(20-x)=4000,
解得:x=15,
∵k=1080>0,
∴y随x的增大而增大,
故x的最大值为15,此时y最大为:1080×15+20000=36200(元).
y=3×800x-240x+5×200(20-x)-80x
=1080x+20000;
(2)∵王大爷有农田20块和现金4000元,由图表可得:
∴240x+80(20-x)=4000,
解得:x=15,
∵k=1080>0,
∴y随x的增大而增大,
故x的最大值为15,此时y最大为:1080×15+20000=36200(元).
点评:此题主要考查了一次函数的应用以及以及一次函数增减性,得出函数解析式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
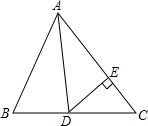 如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.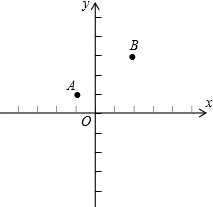 在直角坐标系中,有两点A(-1,1),B(2,3)
在直角坐标系中,有两点A(-1,1),B(2,3) 如图,P是Rt△ABC的斜边BC上异于B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有
如图,P是Rt△ABC的斜边BC上异于B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有 如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+
如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+