题目内容
 如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+
如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+| 1 |
| 2 |
考点:三角形的内切圆与内心
专题:证明题
分析:先根据内心的性质得IB平分∠ABC,IC平分∠ACB,则∠CBI=
∠ABC,∠BCI=
∠ACB,即∠CBI+∠BCI=
(∠ABC+∠ACB),再根据三角形内角和定理得∠CBI+∠BCI=180°-∠BIC,∠ABC+∠ACB=180°-∠BAC,于是有180°-∠BIC=
(180°-∠BAC),然后整理即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵⊙I内切于△ABC,
∴IB平分∠ABC,IC平分∠ACB,
∴∠CBI=
∠ABC,∠BCI=
∠ACB,
∴∠CBI+∠BCI=
(∠ABC+∠ACB),
∵∠CBI+∠BCI=180°-∠BIC,
∠ABC+∠ACB=180°-∠BAC,
∴180°-∠BIC=
(180°-∠BAC),
∴∠BIC=90°+
∠BAC.
∴IB平分∠ABC,IC平分∠ACB,
∴∠CBI=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBI+∠BCI=
| 1 |
| 2 |
∵∠CBI+∠BCI=180°-∠BIC,
∠ABC+∠ACB=180°-∠BAC,
∴180°-∠BIC=
| 1 |
| 2 |
∴∠BIC=90°+
| 1 |
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
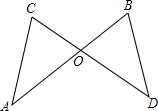 如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )| A、1 | B、3 | C、4 | D、5 |
 如图,已知AB是⊙O的直径,弦CD垂直平分半径OB,垂足为E,∠CDB=30°,OE=1,求图中阴影部分的面积.
如图,已知AB是⊙O的直径,弦CD垂直平分半径OB,垂足为E,∠CDB=30°,OE=1,求图中阴影部分的面积. 如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为
如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为 如图,在等腰梯形ABCD中,AD∥BC,AB=CD=AD=2cm,∠BAD=120°,P为AD的中点,在直线AD下方作∠BPE=120°,使边PE与等腰梯形的某一边所在直线相交于点E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD=AD=2cm,∠BAD=120°,P为AD的中点,在直线AD下方作∠BPE=120°,使边PE与等腰梯形的某一边所在直线相交于点E.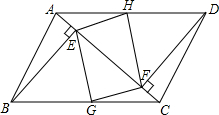 如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远.
如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远.