题目内容
如图，P是Rt△ABC的斜边BC上异于B、C的一点，过点P作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线共有考点：相似三角形的判定
专题：
分析：过点P作直线与另一边相交，使所得的三角形与原三角形有一个公共角，只要再作一个直角就可以．
解答：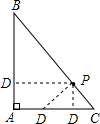
解：由于△ABC是直角三角形，
过P点作直线截△ABC，则截得的三角形与△ABC有一公共角，
所以只要再作一个直角即可使截得的三角形与Rt△ABC相似，
过点P可作AB的垂线、AC的垂线、BC的垂线，共3条直线．
故答案为：3．
解：由于△ABC是直角三角形，过P点作直线截△ABC，则截得的三角形与△ABC有一公共角，
所以只要再作一个直角即可使截得的三角形与Rt△ABC相似，
过点P可作AB的垂线、AC的垂线、BC的垂线，共3条直线．
故答案为：3．
点评：本题主要考查三角形相似判定定理及其运用．解题时运用了两角法（有两组角对应相等的两个三角形相似）来判定两个三角形相似．
练习册系列答案
相关题目
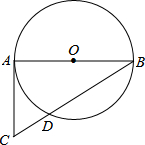已知CA为⊙O的切线，AB是⊙O的直径，BC交⊙O于点D，若AC=6，BD=9，则tan∠DAC=
如图所示，若△ABE≌△ACF，且AB=5，AE=3，则EC的长为
如图，在等腰梯形ABCD中，AD∥BC，AB=CD=AD=2cm，∠BAD=120°，P为AD的中点，在直线AD下方作∠BPE=120°，使边PE与等腰梯形的某一边所在直线相交于点E．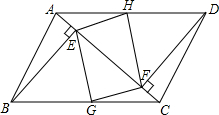
如图是某市一公园的路面示意图，其中四边形ABCD是平行四边形，BE⊥AC，DF⊥AC，E、F是垂足，G、H分别是BC、AD的中点，连接EG、GF、FH、HE为公园中小路．问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地，谁的路程远．
如图，P是半径为2的⊙O外一点，PB是⊙O的切线，B为切点，弦BC∥OA，且BC=2，求图中阴影部分面积．