题目内容
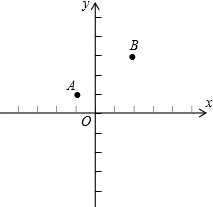 在直角坐标系中,有两点A(-1,1),B(2,3)
在直角坐标系中,有两点A(-1,1),B(2,3)(1)若M为y轴上一点,且MA=MB,求M的坐标;
(2)若N为x轴上一点,且NA+NB最小,求N的坐标.
考点:一次函数综合题
专题:
分析:(1)根据A(-1,1),B(2,3)两点的坐标求得AB的中点的坐标,用待定系数法求出直线AB的解析式,然后根据解析式设出直线AB的垂直平分线的解析式为y=-
x+b,把中点坐标代入即可求得垂直平分线的解析式,再根据y轴上的点的坐标特征求出点M的坐标;
(2)利用轴对称图形的性质可作点A关于x轴的对称点A′,连接A′B,交x轴于点N,点N即为所求.根据A′(-1,-1),B(2,3)两点的坐标用待定系数法求出直线A′B的解析式,再根据x轴上的点的坐标特征求出点M的坐标.
| 3 |
| 2 |
(2)利用轴对称图形的性质可作点A关于x轴的对称点A′,连接A′B,交x轴于点N,点N即为所求.根据A′(-1,-1),B(2,3)两点的坐标用待定系数法求出直线A′B的解析式,再根据x轴上的点的坐标特征求出点M的坐标.
解答: 解:(1)∵A(-1,1),B(2,3),
解:(1)∵A(-1,1),B(2,3),
∴AB的中点C的坐标为(
.2),
∴直线AB为y=
x+
,
∴设直线AB的垂直平分线的解析式为y=-
x+b,
把AB的中点的坐标代入得,2=-
×
+b,解得,b=
,
∴M的坐标为(0,
);
(2)点A关于x轴的对称点A′(-1,-1),
直线A′B的解析式为y=
x+
.
点N为直线A′B与x轴的交点,
∴点N的坐标为(-
,0).
 解:(1)∵A(-1,1),B(2,3),
解:(1)∵A(-1,1),B(2,3),∴AB的中点C的坐标为(
| 1 |
| 2 |
∴直线AB为y=
| 2 |
| 3 |
| 5 |
| 3 |
∴设直线AB的垂直平分线的解析式为y=-
| 3 |
| 2 |
把AB的中点的坐标代入得,2=-
| 3 |
| 2 |
| 1 |
| 2 |
| 11 |
| 4 |
∴M的坐标为(0,
| 11 |
| 4 |
(2)点A关于x轴的对称点A′(-1,-1),
直线A′B的解析式为y=
| 4 |
| 3 |
| 1 |
| 3 |
点N为直线A′B与x轴的交点,
∴点N的坐标为(-
| 1 |
| 4 |
点评:此题主要考查两直线垂直的问题,轴对称--最短路线问题,综合运用了一次函数的知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC,求作一点P,使P到三角形三边的距离相等,则点P是( )
| A、三边中垂线的交点 |
| B、三边的高线的交点 |
| C、三边中线的交点 |
| D、三个内角的角平分线的交点 |
下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是( )
| A、5cm,12cm,13cm | ||||
B、1cm,1cm,
| ||||
C、1cm,2cm,
| ||||
D、
|
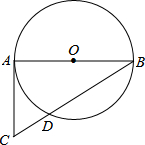 已知CA为⊙O的切线,AB是⊙O的直径,BC交⊙O于点D,若AC=6,BD=9,则tan∠DAC=
已知CA为⊙O的切线,AB是⊙O的直径,BC交⊙O于点D,若AC=6,BD=9,则tan∠DAC= 如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为
如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为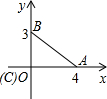 以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为
以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为