题目内容
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a、b、c,根据下列条件,求出直角三角形的其它元素(角度精确到1°)
(1)已知a=4,b=8;
(2)已知b=10,∠B=60°;
(3)已知c=20,∠A=60°.
(1)已知a=4,b=8;
(2)已知b=10,∠B=60°;
(3)已知c=20,∠A=60°.
考点:解直角三角形
专题:计算题
分析:(1)先利用勾股定理计算出c,再利用正切的定义求出∠A,然后利用互余计算∠B;
(2)先利用互余计算出∠A,再利用正切的定义求出a,利用含30度对的边等于斜边的一半得到c的值;
(3)先利用互余计算出∠B,再利用含30度对的边等于斜边的一半得到b的值,然后利用正切的定义求出a.
(2)先利用互余计算出∠A,再利用正切的定义求出a,利用含30度对的边等于斜边的一半得到c的值;
(3)先利用互余计算出∠B,再利用含30度对的边等于斜边的一半得到b的值,然后利用正切的定义求出a.
解答:解:(1)c=
=
4=4
,
∵tanA=
=
=0.5,
∴∠A≈27°,
∴∠B=90°-∠A=63°;
(2)∠A=90°-∠B=90°-60°=30°;
∵tanA=
∴a=10•tan30°=10•
=
;
c=2a=
;
(3)∠B=90°-∠A=90°-60°=30°;
b=
c=
×10=5,
∵tanA=
,
∴a=5•tan60°=5
.
| a2+b2 |
| 42+82 |
| 5 |
∵tanA=
| a |
| b |
| 4 |
| 8 |
∴∠A≈27°,
∴∠B=90°-∠A=63°;
(2)∠A=90°-∠B=90°-60°=30°;
∵tanA=
| a |
| b |
∴a=10•tan30°=10•
| ||
| 3 |
10
| ||
| 3 |
c=2a=
20
| ||
| 3 |
(3)∠B=90°-∠A=90°-60°=30°;
b=
| 1 |
| 2 |
| 1 |
| 2 |
∵tanA=
| a |
| b |
∴a=5•tan60°=5
| 3 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
等腰三角形的两边分别为5和8,那么它的周长是( )
| A、13 | B、18 |
| C、21 | D、18或21 |
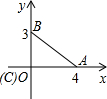 以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为
以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为 如图,P是半径为2的⊙O外一点,PB是⊙O的切线,B为切点,弦BC∥OA,且BC=2,求图中阴影部分面积.
如图,P是半径为2的⊙O外一点,PB是⊙O的切线,B为切点,弦BC∥OA,且BC=2,求图中阴影部分面积.