题目内容
设一个矩形长为x,宽为y,若其面积为2,则y与x函数关系的图象在 象限.
考点:反比例函数的应用
专题:
分析:先根据矩形的面积=长×宽列出关系式,变形得到y与x的函数关系式,再根据自变量的取值范围,确定函数所在的象限.
解答:解:∵一个矩形长为x,宽为y,若其面积为2,
∴xy=2,
∴y=
,
∴y是x的反比例函数,
∵x>0,y>0,
∴反比例函数y=
(x>0)的图象在第一象限.
故答案为:第一.
∴xy=2,
∴y=
| 2 |
| x |
∴y是x的反比例函数,
∵x>0,y>0,
∴反比例函数y=
| 2 |
| x |
故答案为:第一.
点评:本题考查了反比例函数的应用,根据矩形面积公式求出y与x的函数关系式是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
等腰三角形的两边分别为5和8,那么它的周长是( )
| A、13 | B、18 |
| C、21 | D、18或21 |
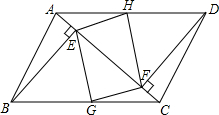 如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远.
如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远.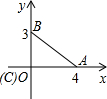 以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为
以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为